On block Behrend sequences
Published online by Cambridge University Press: 24 October 2008
Extract
Let A be a strictly increasing sequence of integers exceeding 1 and let
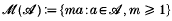
denote its set of multiples. We say that A is a Behrend sequence if M(A) has asymptotic density 1. The theory of sets of multiples was first developed in the late thirties, under the influence of Erdős, Besicovitch, and others. An account of the classical notions is presented in the book of Halberstam and Roth (1966), and recent progress in the area may be found in Hall and Tenenbaum [7], Erdős and Tenenbaum [4], Ruzsa and Tenenbaum [9]. As underlined by Erdős in [3], one of the central problems in the field is that of finding general criteria to decide whether a given sequence A is Behrend.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 120 , Issue 2 , August 1996 , pp. 355 - 367
- Copyright
- Copyright © Cambridge Philosophical Society 1996
References
REFERENCES
- 2
- Cited by


