Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T16:32:14.001Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of probability distributions

Published online by Cambridge University Press:  24 October 2008

S. Chandrasekhar
S. Chandrasekhar
Affiliation:
Yerkes ObservatoryWilliams Bay, Wisconsin
Get access Rights & Permissions [Opens in a new window]

Extract

1. The statement of the problem. A problem which arises in certain physical (5) and astronomical (1, 3) contexts relates to the probability distribution of the infinite sum

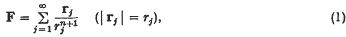
where the rj's are the position vectors from a fixed origin of an infinite uniform Poisson distribution of points with a given constant mean space density N. While certain special cases of the sum (1) have been considered in the literature (cf. (2)) the study of the general case discloses properties of a class of probability distributions which appear to have some interest. For example, we shall show that the probability distribution of F exists only for 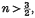that the moments of F (= |F|) exist only for orders 0 ≤ p < 3/n, and finally that an explicit formula can be given for all the finite moments.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 2 , April 1949 , pp. 219 - 224
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Chandrasekhar, S.Astrophys. J. 94 (1941), 511.CrossRefGoogle Scholar
(2)Chandrasekhar, S.Rev. Mod. Phys. 15 (1943), 1.CrossRefGoogle Scholar
(3)Chandrasekhar, S.Astrophys. J. 99 (1944), 25.CrossRefGoogle Scholar
(4)Hertz, P.Math. Ann. 67 (1909), 387.CrossRefGoogle Scholar
(5)Holtsmark, J.Ann. Phys., Lpz., 58 (1919), 577.CrossRefGoogle Scholar