Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Thorisson, Hermann
1986.
Semi-Markov Models.
p.
351.
Niemiro, Wojciech
1995.
Tail events of simulated annealing Markov chains.
Journal of Applied Probability,
Vol. 32,
Issue. 4,
p.
867.
Niemiro, Wojciech
1995.
Tail events of simulated annealing Markov chains.
Journal of Applied Probability,
Vol. 32,
Issue. 4,
p.
867.
Cohn, Harry
and
Fielding, Mark
1999.
Simulated Annealing: Searching for an Optimal Temperature Schedule.
SIAM Journal on Optimization,
Vol. 9,
Issue. 3,
p.
779.


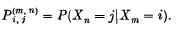
 converges for any
converges for any  , then
, then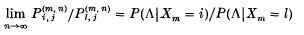
 , whereas if
, whereas if  converges, then
converges, then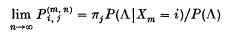
 and
and  . The behaviour of transition probabilities between various groups of states is studied and criteria for recurrence and transience are given.
. The behaviour of transition probabilities between various groups of states is studied and criteria for recurrence and transience are given.