Hostname: page-component-5cf477f64f-mgq6s Total loading time: 0 Render date: 2025-04-03T11:33:35.132Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical sequence and a family of polynomials arising from a question of completeness

Published online by Cambridge University Press:  24 October 2008

L. E. Fraenkel
L. E. Fraenkel
Affiliation:
University of Sussex
Get access Rights & Permissions [Opens in a new window]

Extract

This paper concerns, in the first instance, a sequence {t(1), t(2), t(3), …} of positive numbers denned successively by

where k ∈ ℕ = {1,2,3,…} and

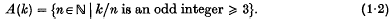
Thus, when k is odd, A(k) consists of those divisors of k that do not exceed k/3; when k is even, A (k) consists of those even divisors n of k that make k/n odd and do not exceed k/3. The sets A(k) are listed in Table 1 for k ≤ 105; the numbers t(1) to t(10) are 1, 1, 4/3, 1, 6/5, 4/3, 8/7, 1, 14/9, 6/5.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 3 , November 1980 , pp. 469 - 481
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bochner, S. and Martin, W. T.Several complex variables (Princeton, University Press, 1948).Google Scholar
(2)Fraenkel, L. E.Completeness properties in L 2 of the eigenfunctions of two semi-linear differential operators. Math. Proc. Cambridge Philos. Soc. 88 (1980) 451–468.Google Scholar
(3)Macmahon, P. A.Combinatory analysis, vols. I and II (Cambridge, University Press, 1915, and New York, Chelsea, 1960).Google Scholar
(4)Riordan, J.An introduction to combinatorial analysis (New York, Wiley, 1958).Google Scholar
(5)Whittaker, E. T. and Watson, G. N.Modern analysis (Cambridge, University Press, 1927).Google Scholar