Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-24T06:50:57.194Z Has data issue: false hasContentIssue false
  • English
  • Français

Notes on iterative processes

Published online by Cambridge University Press:  24 October 2008

D. R. Hartree
D. R. Hartree
Affiliation:
Cavendish LaboratoryCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

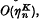If ηn is the error in the result of repeating an iterative process n times, and ηn+1 is the iterative process is called Kth order. It is shown that if for a given equation there is an iterative process of the (K + 1)th order, the iterative process of the Kth order is not unique, and conversely if an iterative process of the Kth order is not unique, it is generally possible to construct from two of the Kth order processes a process of the (K + 1)th order. As an example, three second-order processes for a square root are exhibited, and a third-order process is derived from two of them.

Iterative processes for positive and negative integer roots are given, of kinds suitable for use on machines in which division is a relatively slow process and one to be used sparingly. It is shown how a second-order process can be derived from the results of two repetitions of a first-order process. The extension of this iterative process for the solution of differential and integral equations is a development which is urgently required.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 2 , April 1949 , pp. 230 - 236
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)See Hartree, D. R. Nature, London, 158 (1946), 500.CrossRefGoogle Scholar
(2)Aiken, H. H. and others. Manual of Operation of the Automatic Sequence-controlled Calculator (Harvard University Press, 1946), 176.Google Scholar
(3)Aitken, A. C.Proc. Roy. Soc. Edinburgh, 46 (1925), 289 (see §8) and 57 (1936), 269 (see §8).Google Scholar
(4)Samuelson, P. A.J. Math. Phys. 24 (1945), 131.Google Scholar
(5)Cope, W. F. and Hartree, D. R.Philos. Trans. A, 241 (1948),1 (see §§ 12, 13).Google Scholar