Notes on general topology

Extract

There is a close parallelism between the theories of convergence of directed nets and of filters, in which ‘subnet’ corresponds, in general, to ‘refinement’. With the standard definitions, however (1), pages 65 et seq., this correspondence is not exact, as there is no coarsest net converging to x₀ of which all other nets with the same limit are subnets. (Suppose, for example, that a net X = {x_j,: j ∈ J} in R¹ has both the sequence-net S = {n₋₁; n = 1, 2,…} and the singleton-net {0} as subnets. Then (with an obvious notation), there exist

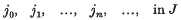
such that j₀ ≥ j_n for all n, while j_n ≥ j₀ for all n ≥ n₀ say. But, given any j ∈ J, there exists n with j_n ≥ j: it follows that j_n ∈ j for all n ≥ n₀ (independent of j); thus X cannot converge to 0. Even if nets with a last member are excluded, a similar result can be obtained by considering the net Y = {y_θ; Θ an ordinal less than ω₁}, where y_θ = 0 for all Θ. If X has both Y and S as subnets we can show that (with a similar notation) there exists Θ₀ such that Θ ≥ Θ₀ implies j_θ ≥ all j_n, but also n₀ such that n ≥ n₀ implies 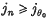; the rest is as before.) Moreover, the theory of convergence classes, (l), pages 73 et seq., contains a condition (Kelley's condition (c)) whose analogue need not be separately stated for filters. These differences can be removed by adopting a wider definition of subnet, a course which does not seem unnatural, inasmuch as the standard definition is already wider than the ‘obvious’ one, and our proposed definition is equivalent to the standard one in the special case of sequences.