Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T02:11:17.195Z Has data issue: false hasContentIssue false
  • English
  • Français

Notes on Fourier series (V): Summability (R1)

Published online by Cambridge University Press:  24 October 2008

G. H. Hardy  and
W. W. Rogosinski
G. H. Hardy
Affiliation:
Trinity CollegeCambridge
W. W. Rogosinski
Affiliation:
King's CollegeNewCastle-on-Tyne
Get access Rights & Permissions [Opens in a new window]

Extract

1·1. There is a familiar method of summation of series usually called the method (R, 1), or sometimes Lebesgue's method. If sn = u0 + u1 + … + un and, as it will be convenient to suppose throughout, u0 = 0, then

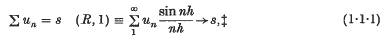
when h → + 0§ the convergence of the series for small positive h is presupposed. The method is not 'regular'; there are convergent series not summable (R, 1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 2 , April 1949 , pp. 173 - 185
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hardy, G. H. and Littlewood, J. E.Math. Z. 19 (1923), 67–96.CrossRefGoogle Scholar
(2)Hardy, G. H. and Rogosinski, W. W.Fourier Series (Cambridge, 1944).Google Scholar
(3)Hardy, G. H. and Rogosinski, W. W.Proc. Cambridge Phil. Soc. 43 (1947), 10–25.CrossRefGoogle Scholar
(4)Kuttner, B.Proc. London Math. Soc. (2), 40 (1936), 524–540.CrossRefGoogle Scholar
(5)Zygmund, A.Trigonometrical series (Warsaw, 1935).Google Scholar