Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T13:16:34.325Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the diophantine equation (xm − l) / (x − 1) = yn + l

Published online by Cambridge University Press:  24 October 2008

Le Maohua
Le Maohua
Affiliation:
Department of Mathematics, Hunan Normal University, Changsha, Hunan, P.R., China
Get access Rights & Permissions [Opens in a new window]

Extract

Let ℤ, ℕ, ℚ denote the sets of integers, positive integers and rational numbers, respectively. Solutions (x, y, m, n) of the equation (1) have been investigated in many papers:

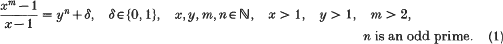
Let ω(m), ρ(m) denote the number of distinct prime factors and the greatest square free factor of m, respectively. In this note we prove the following results.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 116 , Issue 3 , November 1994 , pp. 385 - 389
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cassels, J. W. S.. On the equation a x−b v = 1 II. Proc. Cambridge Philos. Soc. 56 (1960), 97–103.CrossRefGoogle Scholar
[2]Domar, Y.. On the diophantine equation |Ax n−By n| = l, n ≥ 5. Math. Scand. 2 (1954), 29–32.CrossRefGoogle Scholar
[3]Inkeri, K.. On the diophantine equation a(x n − l)/(x − 1) = y m. Acta Arith. 21 (1972), 299–311.CrossRefGoogle Scholar
[4]Laurent, M.. Linear forms in the two logarithms and interpolation determinants. Linear Independence of Logarithms of Algebraic Numbers (M. Waldschmidt). Appendix, Madras, 1992. (See also M. Laurent. Linear forms in two logarithms and interpolation determinants. Acta Arith. 66 1994), (181–199.)CrossRefGoogle Scholar
[5]Ljunggren, W.. On an improvement of a theorem of T. Nagell concerning the diophantine equation Ax 3 + By 3 = C. Math. Scand. I (1953), 297–309.CrossRefGoogle Scholar
[6]Nagell, T.. Note sur l'équation indéterminée (x n − 1)/(x − 1) = y q. Norsk Mat. Tidsskr. 1 (1920), 75–78.Google Scholar
[7]Shorey, T. N.. Perfect powers in values of certain polynomials at integer points. Proc. Cambridge Philos. Soc. 99 (1986), 195–207.CrossRefGoogle Scholar
[8]Shorey, T. N.. On the equation z q = (x n − 1)/(x − 1). Indag.Math. 48 (1986), 345–351.CrossRefGoogle Scholar
[9]Shorey, T. N.. Some exponential diophantine equations (II). Number Theory and Related Topics (Tata Institute of Fundamental Research, Bombay, 1988).Google Scholar
[10]Siegel, C. L.. Die Gleichung ax n − by n = c. Math. Ann. 144 (1937), 57–68.CrossRefGoogle Scholar