A note on the convergence of multi-point Taylor's series

Extract

Series which behave rather like Taylor's series at more than, one point are described and their convergence is discussed briefly.

Let

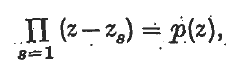
where z, z_s are complex numbers and z_s are the points, (the base points)about which a function is to be expanded. They need not be distinct. p{z) is a polynomial of degree n. in z. Assume first that z, z_s are real and the z_s are distinct. Then polynomials p_n-1,_t(z) may be chosen so that the series

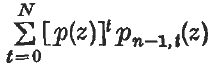
has contact of order N at the points z_s with any specified real function which has N derivatives at these points. This is proved merely by rearranging the simplest polynomial in z which has contact of order N with/(z) at z = z_s. The term given by t = 0 in (2) allows the series to have the values f(z_s) at z = z_s; adding the term for t = 1 does not alter the values of the series at z = z_s; it allows the series to have a derivative with values f′(z_s) at z = z; similarly adding the term for t = 2 does not alter the value of the series or its first derivative at z = z_s, it allows the series to have a second derivative with values f″{z_s) at z = z_s; and so on. If m of the z_s coincide then f(z) has mN + m− 1 derivatives there and contact is of order mN + m− 1. If z, z_s are complex the result is seen to be valid subject to the obvious generalization of ‘ contact of the ith order’ to complex variables and functions.