Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T02:41:03.564Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on integral functions

Published online by Cambridge University Press:  24 October 2008

R. E. A. C. Paley
R. E. A. C. Paley
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let f(z) denote an integral function of finite order ρ. We write

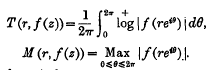
It has been shown that

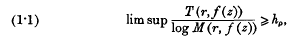
where hρ is a constant which depends only on ρ. We are naturally led to enquire whether some equation of the form (1.1) may be true with lim sup replaced by lim inf. In this note we show that the reverse is true. We construct an integral function of zero order for which

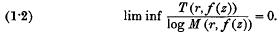
The proof may easily be modified to construct a function of any finite order or of infinite order for which (1.2) is satisfied.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 28 , Issue 3 , July 1932 , pp. 262 - 265
Copyright
Copyright © Cambridge Philosophical Society 1932

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* For ρ ≤ ½, the best possible value of h ρ is known to be (sin πρ)/πρ. For ρ ≤ ½ it seems likely that the correct constant is 1/(πρ), which is the value for the function (2.1), with a = 1/ρ. Miss M. L. Cartwright has shown me a proof of (1.1) with a constant h ρ which for large values of ρ is asymptotically 1/(2eρ).

† See e.g. Bieberbach, L., Lehrbuch der Functionentheorie, 2 (1927), 265–269.Google Scholar