Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T13:13:20.315Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on Cusick's theorem on units in totally real cubic fields

Published online by Cambridge University Press:  24 October 2008

H. J. Godwin
H. J. Godwin
Affiliation:
Department of Statistics and Computer Science, Royal Holloway College, Egham, Surrey, TW20 0EX
Get access Rights & Permissions [Opens in a new window]

Extract

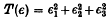Let ε = ε1, with conjugates ε2, ε3, be a unit in a totally real cubic field, and let . Let ε be a unit for which T (ε) is least and let η be a unit, not a power of ε, for which T(η) is least. It was shown by Cusick[l] that ε,η form a pair of fundamental units under certain conditions. The purpose of the present note is to show that these conditions are unnecessary and that ε, η form a pair of fundamental units in all cases.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 95 , Issue 1 , January 1984 , pp. 1 - 2
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Cusick, T. W.. Finding fundamental units in cubic fields. Math. Proc. Cambridge Philos. Soc. 92 (1982), 385–389.CrossRefGoogle Scholar
[2] Godwin, H. J.. The determination of units in totally real cubic fields. Proc. Cambridge Philos. Soc. 56 (1960), 318–321.CrossRefGoogle Scholar