Norm and spectral radius for algebraic elements of a Banach algebra
Published online by Cambridge University Press: 24 October 2008
Extract
The purpose of this note is to show that, for any algebraic element a of a Banach algebra and certain analytic functions f, one can give an upper bound for ‖f(a)‖ in terms of ‖a‖ and the spectral radius ρ(a) of a. To illustrate the nature of the result, consider the norms of powers of an element a of unit norm. In general, the spectral radius formula
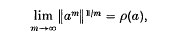
contains all that can be said (that is, the limit ρ(a) can be approached arbitrarily slowly). If we have the additional information that a is algebraic of degree n we can say a good deal more. In the case of a C*-algebra we have the neat result that, if ‖a‖ ≤ 1,
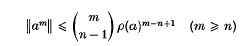
(see Theorem 2), while for a general Banach algebra we have at least
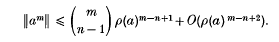
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 1 , July 1980 , pp. 129 - 133
- Copyright
- Copyright © Cambridge Philosophical Society 1980
References
REFERENCES
- 3
- Cited by


