Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T01:41:02.963Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-injective representations of a closed surface group into PSL(2, )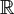

Published online by Cambridge University Press:  10 April 2007

LOUIS FUNAR  and
MAXIME WOLFF
LOUIS FUNAR
Affiliation:
Institut Fourier BP 74, UMR 5582, Université Grenoble I, 38402 Saint-Martin-d'Hères Cedex, France. e-mail: [email protected], [email protected]
MAXIME WOLFF
Affiliation:
Institut Fourier BP 74, UMR 5582, Université Grenoble I, 38402 Saint-Martin-d'Hères Cedex, France. e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let e denote the Euler class on the space 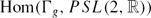of representations of the fundamental group Γg of the closed surface Σg of genus g. Goldman showed that the connected components of 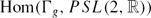are precisely the inverse images e−1(k), for 2−2g≤ k≤ 2g−2, and that the components of Euler class 2−2g and 2g−2 consist of the injective representations whose image is a discrete subgroup of 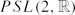. We prove that non-faithful representations are dense in all the other components. We show that the image of a discrete representation essentially determines its Euler class. Moreover, we show that for every genus and possible corresponding Euler class, there exist discrete representations.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 142 , Issue 2 , March 2007 , pp. 289 - 304
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Breuillard, E., Gelander, T., Souto, J. and Storm, P.. Dense surface groups in Lie groups, in preparation.Google Scholar
[2] Brown, K.. Cohomology of Groups, GTM 87 (Springer-Verlag, 1994).Google Scholar
[3] Culler, M. and Shallen, P. B.. Varieties of group representations and splittings of 3-manifolds. Ann. of Math. 117 (1983), 109–146.CrossRefGoogle Scholar
[4] DeBlois, J. and Kent, R. P. IV. Surface groups are frequently faithful. Duke Math. J. 131 (2006), 351–362.CrossRefGoogle Scholar
[5] Gallo, D., Kapovich, M. and Marden, A.. The monodromy groups of Schwarzian equations on closed Riemann surfaces. Ann. of Math. 151 (2000), 625–704.CrossRefGoogle Scholar
[6] Ghys, E.. Classe d'Euler et minimale exceptionnel. Topology 26 (1987), 93–105.CrossRefGoogle Scholar
[7] Glutsyuk, A.. Instability of nondiscrete free subgroups in Lie groups, math.DS/0409556, (2004).Google Scholar
[8] Goldman, W.. Discontinuous groups and the Euler class. PhD Thesis (Berkeley, 1980).Google Scholar
[9] Goldman, W.. The symplectic nature of fundamental groups of surfaces. Adv. in Math. 54 (1984), 200–225.CrossRefGoogle Scholar
[10] Goldman, W.. Topological components of spaces of representations. Invent. Math. 93 (1988), 557–607.CrossRefGoogle Scholar
[11] Hitchin, N. J.. The self-duality equations on a Riemann surface. Proc. London Math. Soc. (3) 55 (1987), 59–126.CrossRefGoogle Scholar
[12] Katok, S.. Fuchsian groups. Chicago Lectures Math. (1992).Google Scholar
[13] Magnus, W.. Rational representations of Fuchsian groups and non-parabolic subgroups of the modular group. Nachr. Akad. Wiss. Gottingen Math.-Phys. K.I. II (1973), 179–189.Google Scholar
[14] Milnor, J. W.. On the existence of a connection with curvature zero. Comment. Math. Helv. 32 (1958), 215–223.CrossRefGoogle Scholar
[15] Tan, S. P.. Branched CP 1-structures on surfaces with prescribed real holonomy. Math. Ann. 300 (1994), 649–667.CrossRefGoogle Scholar
[16] Wood, J. W.. Bundles with totally disconnected structure group. Comment. Math. Helv. 51 (1971), 183–199.Google Scholar