A non-commutative Gel'fand-Naimark theorem
Published online by Cambridge University Press: 24 October 2008
Extract
This paper presents a straightforward proof of the Gel'fand-Naimark theorem for non-commutative C*-algebras with identity, established by Dauns and Hofmann(2) in the context of fields of C*-algebras, by considering instead C*-algebras in categories of sheaves. The proof differs from that of (2,3,4) in obtaining an isometric *-isomorphism
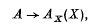
from the C*-algebra A to the C*-algebra of sections of a C*-algebra Ax in the category of sheaves on the maximal ideal space X of the centre of A, without invoking any arguments which involve completeness (3, Theorem 7·9). Instead, the results of (7) yield immediately the existence of an algebraic isomorphism, the compactness of the maximal ideal space X then being used to prove that Ax is indeed a C*-algebra in the category of sheaves on X and that the isomorphism is isometric. One recovers the representation of (2) by noting (8) that any C*-algebra in the category of sheaves on X is isomorphic to the sheaf of sections of a canonical field of C*-algebras on X.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 3 , November 1980 , pp. 425 - 428
- Copyright
- Copyright © Cambridge Philosophical Society 1980
References
REFERENCES
- 4
- Cited by


