Nielsen's commutator test for two-generator groups
Published online by Cambridge University Press: 24 October 2008
Extract
Nielsen [14] gave the following commutator test for an endomorphism of the free group F = F2 = 〈x, y; Ø〉 to be an automorphism: an endomorphism ø: F → F is an automorphism if and only if the commutator [ø(x), ø(y)] is conjugate in F to [x, y]±1. He obtained this test as a corollary to his well-known result that every IA-automorphism of F (i.e. one which fixes F modulo its commutator subgroup) is an inner automorphism. Bachmuth et al. [4] have proved that IA-automorphisms of most two-generator groups of the type F/R′ are inner, and it becomes natural to ask if Nielsen's commutator test remains valid for those groups as well. Durnev[7] considered this question for the free metabelian group F/F″ and confirmed the validity of the commutator test in this case. Here we prove that Nielsen's test does not hold for a large class of F/R′ groups (Theorem 3·1) and, as a corollary, deduce that it does not hold for any non-metabelian solvable group of the form F/R″ (Corollary 3·2). In view of our Theorem 3·1, Nielsen's commutator test in these situations seems to have less appeal than his result that the IA-automorphisms of F are precisely the inner automorphisms of F. We explore some applications of this important result with respect to non-tameness of automorphisms of certain two- generator groups F/R (i.e. automorphisms of F/R which are not induced by those of the free group F). For instance, we show that a two-generator free polynilpotent group F/V, 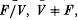 , has non-tame automorphisms except when V = γ2(F) or V = γ3(F), or when V is of the form [yn(U), γ(U)], n ≥ 2 (Theorem 4·2). This complements the results of [9] and [16] rather nicely, and is shown to follow from a more general result (Proposition 4·1). We also include an example of an endomorphism θ: x → xu, y→y of F which induces a non-tame automorphism of F/γ6(F) while the partial derivative ∂(u)/∂(x) is ‘balanced’in the sense of Bryant et al. [5] (Example 4·4). This gives an alternative solution of a problem in [5] which has already been resolved by Papistas [15] in the negative. In our final section, we consider groups of the type F/[R′,F] and, in contrast to groups of the type F/R′, we show that the Nielsen's commutator test does hold in most of these groups (Theorem 5·1). We conclude with a sufficiency condition under which Nielsen's commutator test is valid for a given pair of generating elements ofF modulo [R′,F] (Proposition 5·2).
, has non-tame automorphisms except when V = γ2(F) or V = γ3(F), or when V is of the form [yn(U), γ(U)], n ≥ 2 (Theorem 4·2). This complements the results of [9] and [16] rather nicely, and is shown to follow from a more general result (Proposition 4·1). We also include an example of an endomorphism θ: x → xu, y→y of F which induces a non-tame automorphism of F/γ6(F) while the partial derivative ∂(u)/∂(x) is ‘balanced’in the sense of Bryant et al. [5] (Example 4·4). This gives an alternative solution of a problem in [5] which has already been resolved by Papistas [15] in the negative. In our final section, we consider groups of the type F/[R′,F] and, in contrast to groups of the type F/R′, we show that the Nielsen's commutator test does hold in most of these groups (Theorem 5·1). We conclude with a sufficiency condition under which Nielsen's commutator test is valid for a given pair of generating elements ofF modulo [R′,F] (Proposition 5·2).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 114 , Issue 2 , September 1993 , pp. 295 - 301
- Copyright
- Copyright © Cambridge Philosophical Society 1993
References
REFERENCES
- 10
- Cited by


