Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tricot, Claude
1989.
Porous surfaces.
Constructive Approximation,
Vol. 5,
Issue. 1,
p.
117.
Tricot, Claude
1989.
Constructive Approximation.
p.
117.
Bessis, Daniel
and
Demko, Stephen
1990.
Generalized Apollonian packings.
Communications in Mathematical Physics,
Vol. 134,
Issue. 2,
p.
293.
Mauldin, R.Daniel
and
Urbański, Mariusz
1998.
Dimension and Measures for a Curvilinear Sierpinski Gasket or Apollonian Packing.
Advances in Mathematics,
Vol. 136,
Issue. 1,
p.
26.
Graham, Ronald L.
Lagarias, Jeffrey C.
Mallows, Colin L.
Wilks, Allan R.
and
Yan, Catherine H.
2003.
Apollonian circle packings: number theory.
Journal of Number Theory,
Vol. 100,
Issue. 1,
p.
1.
Kahng, Byungik
2004.
Dynamics of kaleidoscopic maps.
Advances in Mathematics,
Vol. 185,
Issue. 1,
p.
178.
Botet, Robert
Kwok, Sylvie
and
Cabane, Bernard
2021.
Filling space with polydisperse spheres in a non-Apollonian way.
Journal of Physics A: Mathematical and Theoretical,
Vol. 54,
Issue. 19,
p.
195201.


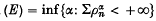 proved by Boyd
proved by Boyd 