Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T13:22:40.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Multi-indexing and multiple clustering

Published online by Cambridge University Press:  24 October 2008

Z. A. Melzak
Z. A. Melzak
Affiliation:
University of British Columbia, Vancouver
Get access Rights & Permissions [Opens in a new window]

Extract

1. Simple linear clustering. One of the simplest clustering problems is the following: if n points are taken independently and uniformly at random on the interval I = [0, L], what is the probability Q = Q(n, a, L) that no two points are closer than a? The well-known answer

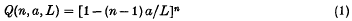
if (n − 1) a ≤ L, and Q = 0 otherwise, can be obtained in a variety of ways. Perhaps the simplest one is the original method of E.C.Molina(5). If x1,…,xn are the abscissas of the n points, then there are n! equiprobable orderings of the xi's consistent with the condition that no two points are closer than a. The probability of each one is

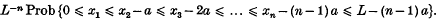
Let yi = xi − (i − 1) a for i = 1,…,n, then the above becomes

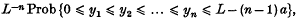
which is

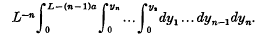
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 2 , September 1979 , pp. 313 - 338
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Efron, B.Ann. Math. Stat. 38 (1967), 298.CrossRefGoogle Scholar
(2)Jung, H. W. E.J. reine angew. Math. 123 (1901), 241.Google Scholar
(3)Melzak, Z. A.Quart. Appl. Math. 20 (1962), 151.CrossRefGoogle Scholar
(4)Melzak, Z. A.Bell System Tech. J. 47 (1968), 1105.CrossRefGoogle Scholar
(5)Molina, E. C.Trans. A.I.E.E. 44 (1929), 294.Google Scholar
(6)Riordan, J.An introduction to combinatorial analysis (New York, John Wiley, 1958).Google Scholar