Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hunt, Brian R
and
Kaloshin, Vadim Yu
1997.
How projections affect the dimension spectrum of fractal measures.
Nonlinearity,
Vol. 10,
Issue. 5,
p.
1031.
Olsen, L.
1999.
Measurability of multifractal measure functions and multifractal dimension functions.
Hiroshima Mathematical Journal,
Vol. 29,
Issue. 3,
O'Neil, Toby C.
2000.
The multifractal spectra of projected measures in Euclidean spaces.
Chaos, Solitons & Fractals,
Vol. 11,
Issue. 6,
p.
901.
Olsen, L.
2000.
Fractal Geometry and Stochastics II.
p.
3.
Wójcik, Daniel
Nowak, Andrzej
and
Kuś, Marek
2001.
Dimension of interaction dynamics.
Physical Review E,
Vol. 63,
Issue. 3,
Kenneth, J. Falconer
2002.
Handbook of Measure Theory.
p.
1037.
Attia, Najmeddine
Selmi, Bilel
and
Souissi, Chouhaïd
2017.
Some density results of relative multifractal analysis.
Chaos, Solitons & Fractals,
Vol. 103,
Issue. ,
p.
1.
Menceur, Mohamed
and
Mabrouk, Anouar Ben
2019.
A joint multifractal analysis of vector valued non Gibbs measures.
Chaos, Solitons & Fractals,
Vol. 126,
Issue. ,
p.
203.
Selmi, Bilel
2020.
On the projections of the multifractal packing dimension for $$q>1$$.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 199,
Issue. 4,
p.
1519.
Attia, Najmeddine
and
Selmi, Bilel
2021.
A Multifractal Formalism for Hewitt–Stromberg Measures.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 1,
p.
825.
Attia, Najmeddine
Jebali, Hajer
and
Khlifa, Meriem Ben Hadj
2021.
A Note on Fractal Measures and Cartesian Product Sets.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 44,
Issue. 6,
p.
4383.
Selmi, Bilel
2021.
Multifractal dimensions for projections of measures.
Boletim da Sociedade Paranaense de Matemática,
Vol. 40,
Issue. ,
p.
1.
Ben, Mabrouk
Menceur, Mohamed
and
Selmi, Bilel
2022.
On the mixed multifractal densities and regularities with respect to gauges.
Filomat,
Vol. 36,
Issue. 12,
p.
4225.
MABROUK, ANOUAR BEN
and
FARHAT, ADEL
2022.
MIXED MULTIFRACTAL DENSITIES FOR QUASI-AHLFORS VECTOR-VALUED MEASURES.
Fractals,
Vol. 30,
Issue. 01,
Selmi, Bilel
2022.
Slices of Hewitt–Stromberg measures and co-dimensions formula.
Analysis,
Vol. 42,
Issue. 1,
p.
23.
MABROUK, ANOUAR BEN
and
FARHAT, ADEL
2022.
A MIXED MULTIFRACTAL ANALYSIS FOR QUASI-AHLFORS VECTOR-VALUED MEASURES.
Fractals,
Vol. 30,
Issue. 01,
Attia, Najmeddine
and
Selmi, Bilel
2023.
Different types of multifractal measures in separable metric spaces and their applications.
AIMS Mathematics,
Vol. 8,
Issue. 6,
p.
12889.
Selmi, Bilel
2024.
Subsets of Positive and Finite $$\Psi _t$$-Hausdorff Measures and Applications.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 3,
Achour, Rim
Li, Zhiming
Selmi, Bilel
and
Wang, Tingting
2024.
A multifractal formalism for new general fractal measures.
Chaos, Solitons & Fractals,
Vol. 181,
Issue. ,
p.
114655.
Liu, Yu
Selmi, Bilel
and
Li, Zhiming
2024.
On the mean fractal dimensions of the Cartesian product sets.
Chaos, Solitons & Fractals,
Vol. 180,
Issue. ,
p.
114503.

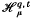 and
and 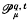 denote the multifractal Hausdorff measure and the multifractal packing measure introduced in [O11] Let μ be a Borel probability merasure on
denote the multifractal Hausdorff measure and the multifractal packing measure introduced in [O11] Let μ be a Borel probability merasure on 


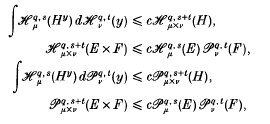 for E ⊆
for E ⊆


 d. Math. Proc. Camb. Phil. Soc. 115 (1994), 527–544.CrossRefGoogle Scholar
d. Math. Proc. Camb. Phil. Soc. 115 (1994), 527–544.CrossRefGoogle Scholar

