Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T01:00:33.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Motion of a sphere through a conducting fluid in the presence of a strong magnetic field

Published online by Cambridge University Press:  24 October 2008

K. Stewartson
K. Stewartson
Affiliation:
Department of MathematicsThe UniversityBristol 8
Get access Rights & Permissions [Opens in a new window]

Abstract

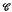The steady motion of a perfectly conducting sphere in an inviscid conducting fluid in the presence of a strong magnetic field is discussed. It is shown that if the fluid velocity is ultimately steady then it is two-dimensional, and a cylinder of fluid whose generators are parallel to the direction of the field moves with the sphere as if solid. The streamlines outside 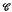are straight lines if the sphere moves in the direction of the field but have to execute sharp turns if it moves at right angles to the field. The motion to be expected in practice is discussed using an analogy.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 52 , Issue 2 , April 1956 , pp. 301 - 316
Copyright
Copyright © Cambridge Philosophical Society 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Batchelor, G. K.Proc. roy. Soc. A, 201 (1950), 405.Google Scholar
(2)Chandrasekhar, S.Proc. roy. Soc. A, 216 (1953), 293.Google Scholar
(3)Dean, W. R.Quart. J. Mech. 7 (1954), 257.Google Scholar
(4)Lehnert, B.Phys. Rev. (2), 94 (1954), 815.CrossRefGoogle Scholar
(5)Michael, D. H.Mathematika, 1 (1954), 131.Google Scholar
(6)Morgan, G. W.Proc. Camb. phil. Soc. 49 (1953), 362.CrossRefGoogle Scholar
(7)Stewartson, K.Proc. Camb. phil. Soc. 48 (1952), 168.Google Scholar
(8)Stewartson, K.Quart. J. Mech. 6 (1953), 141.CrossRefGoogle Scholar
(9)Stuart, J. T.Proc. roy. Soc. A, 221 (1954), 189.Google Scholar
(10)Taylor, G. I.Proc. roy. Soc. A, 93 (1916), 99.Google Scholar
(11)Taylor, G. I.Proc. roy. Soc. A, 102 (1922), 114.Google Scholar
(12)Taylor, G. I.Proc. roy. Soc. A, 104 (1923), 213.Google Scholar
(13)Titchmarsh, E. C.Introduction to the theory of Fourier integrals (Oxford, 1948), p. 339.Google Scholar
(14)Watson, G. N.Theory of Bessel functions (Cambridge, 1944), p. 401.Google Scholar