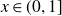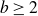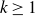1. Introduction
A real number
![]() $x \in (0,1]$
is normal if, informally, for each base
$x \in (0,1]$
is normal if, informally, for each base
![]() $b\ge 2$
, its b-adic expansion contains every finite string with the expected uniform limit frequency (the precise definition is given in the next few lines). It is well known that most numbers x are normal from a measure theoretic viewpoint, see e.g. [
Reference Bergelson, Downarowicz and Misiurewicz5
] for history and generalisations. However, it has been recently shown that certain subsets of nonnormal numbers may have full Hausdorff dimension, see e.g. [
Reference Albeverio, Pratsiovytyi and Torbin1, Reference Barreira and Schmeling4
]. The aim of this work is to show that, from a topological viewpoint, most numbers are not normal in a strong sense. This provides another nonanalogue between measure and category, cf. [
Reference Oxtoby25
].
$b\ge 2$
, its b-adic expansion contains every finite string with the expected uniform limit frequency (the precise definition is given in the next few lines). It is well known that most numbers x are normal from a measure theoretic viewpoint, see e.g. [
Reference Bergelson, Downarowicz and Misiurewicz5
] for history and generalisations. However, it has been recently shown that certain subsets of nonnormal numbers may have full Hausdorff dimension, see e.g. [
Reference Albeverio, Pratsiovytyi and Torbin1, Reference Barreira and Schmeling4
]. The aim of this work is to show that, from a topological viewpoint, most numbers are not normal in a strong sense. This provides another nonanalogue between measure and category, cf. [
Reference Oxtoby25
].
For each
![]() $x \in (0,1]$
, denote its unique nonterminating b-adic expansion by
$x \in (0,1]$
, denote its unique nonterminating b-adic expansion by
with each digit
![]() $d_{b,n}(x) \in \{0,1,\ldots,b-1\}$
, where
$d_{b,n}(x) \in \{0,1,\ldots,b-1\}$
, where
![]() $b\ge 2$
is a given integer. Then, for each string
$b\ge 2$
is a given integer. Then, for each string
![]() ${\boldsymbol{s}}=s_1\cdots s_k$
with digits
${\boldsymbol{s}}=s_1\cdots s_k$
with digits
![]() $s_j \in \{0,1,\ldots,b-1\}$
and each
$s_j \in \{0,1,\ldots,b-1\}$
and each
![]() $n\ge 1$
, write
$n\ge 1$
, write
![]() $\pi_{b,{\boldsymbol{s}},n}(x)$
for the proportion of strings
$\pi_{b,{\boldsymbol{s}},n}(x)$
for the proportion of strings
![]() ${\boldsymbol{s}}$
in the b-adic expansion of x which start at some position
${\boldsymbol{s}}$
in the b-adic expansion of x which start at some position
![]() $\le n$
, i.e.,
$\le n$
, i.e.,
In addition, let
![]() $S_{b}^k$
be the set of all possible strings
$S_{b}^k$
be the set of all possible strings
![]() ${\boldsymbol{s}}=s_1\cdots s_k$
in base b of length k, hence
${\boldsymbol{s}}=s_1\cdots s_k$
in base b of length k, hence
![]() $\#S_{b}^k=b^k$
, and denote by
$\#S_{b}^k=b^k$
, and denote by
![]() ${\boldsymbol{\pi}}^{k}_{b,n}(x)$
the vector
${\boldsymbol{\pi}}^{k}_{b,n}(x)$
the vector
![]() $(\pi_{b,{\boldsymbol{s}},n}(x)\;:\; {\boldsymbol{s}} \in S_{b}^k)$
. Of course,
$(\pi_{b,{\boldsymbol{s}},n}(x)\;:\; {\boldsymbol{s}} \in S_{b}^k)$
. Of course,
![]() ${\boldsymbol{\pi}}^{k}_{b,n}(x)$
belongs to the
${\boldsymbol{\pi}}^{k}_{b,n}(x)$
belongs to the
![]() $(b^k-1)$
-dimensional simplex for each n. However, the components of
$(b^k-1)$
-dimensional simplex for each n. However, the components of
![]() ${\boldsymbol{\pi}}^{k}_{b,n}(x)$
satisfy an additional requirement: if
${\boldsymbol{\pi}}^{k}_{b,n}(x)$
satisfy an additional requirement: if
![]() $k\ge 2$
and
$k\ge 2$
and
![]() ${\boldsymbol{s}}=s_1\cdots s_{k-1}$
is a string in
${\boldsymbol{s}}=s_1\cdots s_{k-1}$
is a string in
![]() $S_b^{k-1}$
, then
$S_b^{k-1}$
, then
where
![]() $s_0{\boldsymbol{s}}$
and
$s_0{\boldsymbol{s}}$
and
![]() ${\boldsymbol{s}}s_k$
stand for the concatened strings (indeed, the above identity is obtained by a double counting of the occurrences of the string
${\boldsymbol{s}}s_k$
stand for the concatened strings (indeed, the above identity is obtained by a double counting of the occurrences of the string
![]() ${\boldsymbol{s}}$
as the occurrences of all possible strings
${\boldsymbol{s}}$
as the occurrences of all possible strings
![]() ${\boldsymbol{s}}s_k$
; or, equivalently, as the occurrences of all possible strings
${\boldsymbol{s}}s_k$
; or, equivalently, as the occurrences of all possible strings
![]() $s_0{\boldsymbol{s}}$
, with the caveat of counting them correctly at the two extreme positions, hence with an error of at most 1). It follows that the set
$s_0{\boldsymbol{s}}$
, with the caveat of counting them correctly at the two extreme positions, hence with an error of at most 1). It follows that the set
![]() $\textrm{L}^k_{b}(x)$
of accumulation points of the sequence of vectors
$\textrm{L}^k_{b}(x)$
of accumulation points of the sequence of vectors
![]() $({\boldsymbol{\pi}}^{k}_{b,n}(x)\;:\; n\ge 1)$
is contained in
$({\boldsymbol{\pi}}^{k}_{b,n}(x)\;:\; n\ge 1)$
is contained in
![]() $\Delta_{b}^k$
, where
$\Delta_{b}^k$
, where
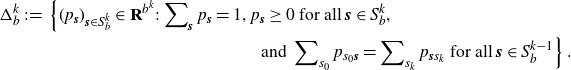 \begin{equation*}\begin{split}\Delta_{b}^k \;:\!=\; \left\{(p_{{\boldsymbol{s}}})_{{\boldsymbol{s}} \in S_{b}^k} \in \textbf{R}^{b^k}:\sum\nolimits_{{\boldsymbol{s}}} p_{{\boldsymbol{s}}}=1, \right. &p_{{\boldsymbol{s}}}\ge 0 \text{ for all }{\boldsymbol{s}} \in S_{b}^k, \\&\left.\text{ and }\sum\nolimits_{s_0}p_{s_0{\boldsymbol{s}}}=\sum\nolimits_{s_k}p_{{\boldsymbol{s}}s_k} \text{ for all }{\boldsymbol{s}} \in S_{b}^{k-1}\right\}.\end{split}\end{equation*}
\begin{equation*}\begin{split}\Delta_{b}^k \;:\!=\; \left\{(p_{{\boldsymbol{s}}})_{{\boldsymbol{s}} \in S_{b}^k} \in \textbf{R}^{b^k}:\sum\nolimits_{{\boldsymbol{s}}} p_{{\boldsymbol{s}}}=1, \right. &p_{{\boldsymbol{s}}}\ge 0 \text{ for all }{\boldsymbol{s}} \in S_{b}^k, \\&\left.\text{ and }\sum\nolimits_{s_0}p_{s_0{\boldsymbol{s}}}=\sum\nolimits_{s_k}p_{{\boldsymbol{s}}s_k} \text{ for all }{\boldsymbol{s}} \in S_{b}^{k-1}\right\}.\end{split}\end{equation*}
Then x is said to be normal if
Hence, if x is normal, then
![]() $\textrm{L}_{b}^k(x)=\{(1/b^{k}, \ldots, 1/b^{k})\}$
. Olsen proved in [
Reference Olsen23
] that the subset of nonnormal numbers with maximal set of accumulation points is topologically large:
$\textrm{L}_{b}^k(x)=\{(1/b^{k}, \ldots, 1/b^{k})\}$
. Olsen proved in [
Reference Olsen23
] that the subset of nonnormal numbers with maximal set of accumulation points is topologically large:
Theorem 1·1. The set
![]() $\{x \in (0,1]\;:\; \textrm{L}_{b}^k(x)=\Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager.
$\{x \in (0,1]\;:\; \textrm{L}_{b}^k(x)=\Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager.
First, we strenghten Theorem 1·1 by showing that the set of accumulation points
![]() $\textrm{L}_{b}^k(x)$
can be replaced by the much smaller subset of accumulation points
$\textrm{L}_{b}^k(x)$
can be replaced by the much smaller subset of accumulation points
![]() ${\boldsymbol{\eta}}$
such that every neighbourhood of
${\boldsymbol{\eta}}$
such that every neighbourhood of
![]() ${\boldsymbol{\eta}}$
contains “sufficiently many” elements of the sequence, where “sufficiently many” is meant with respect to a suitable ideal
${\boldsymbol{\eta}}$
contains “sufficiently many” elements of the sequence, where “sufficiently many” is meant with respect to a suitable ideal
![]() $\mathcal{I}$
of subsets of the positive integers
$\mathcal{I}$
of subsets of the positive integers
![]() $\textbf{N}$
; see Theorem 2·1. Hence, Theorem 1·1 corresponds to the case where
$\textbf{N}$
; see Theorem 2·1. Hence, Theorem 1·1 corresponds to the case where
![]() $\mathcal{I}$
is the family of finite sets.
$\mathcal{I}$
is the family of finite sets.
Then, for certain ideals
![]() $\mathcal{I}$
(including the case of the family of asymptotic density zero sets), we even strenghten the latter result by showing that each accumulation point
$\mathcal{I}$
(including the case of the family of asymptotic density zero sets), we even strenghten the latter result by showing that each accumulation point
![]() ${\boldsymbol{\eta}}$
can be chosen to be the limit of a subsequence with “sufficiently many” indexes (as we will see in the next Section, these additional requirements are not equivalent); see Theorem 2·3. The precise definitions, together with the main results, follow in Section 2.
${\boldsymbol{\eta}}$
can be chosen to be the limit of a subsequence with “sufficiently many” indexes (as we will see in the next Section, these additional requirements are not equivalent); see Theorem 2·3. The precise definitions, together with the main results, follow in Section 2.
2. Main results
An ideal
![]() $\mathcal{I}\subseteq \mathcal{P}(\textbf{N})$
is a family closed under finite union and subsets. It is also assumed that
$\mathcal{I}\subseteq \mathcal{P}(\textbf{N})$
is a family closed under finite union and subsets. It is also assumed that
![]() $\mathcal{I}$
contains the family of finite sets Fin and it is different from
$\mathcal{I}$
contains the family of finite sets Fin and it is different from
![]() $\mathcal{P}(\textbf{N})$
. Every subset of
$\mathcal{P}(\textbf{N})$
. Every subset of
![]() $\mathcal{P}(\textbf{N})$
is endowed with the relative Cantor-space topology. In particular, we may speak about
$\mathcal{P}(\textbf{N})$
is endowed with the relative Cantor-space topology. In particular, we may speak about
![]() $G_\delta$
-subsets of
$G_\delta$
-subsets of
![]() $\mathcal{P}(\textbf{N})$
,
$\mathcal{P}(\textbf{N})$
,
![]() $F_\sigma$
-ideals, meager ideals, analytic ideals, etc. In addition, we say that
$F_\sigma$
-ideals, meager ideals, analytic ideals, etc. In addition, we say that
![]() $\mathcal{I}$
is a P-ideal if it is
$\mathcal{I}$
is a P-ideal if it is
![]() $\sigma$
-directed modulo finite sets, i.e., for each sequence
$\sigma$
-directed modulo finite sets, i.e., for each sequence
![]() $(S_n)$
of sets in
$(S_n)$
of sets in
![]() $\mathcal{I}$
there exists
$\mathcal{I}$
there exists
![]() $S \in \mathcal{I}$
such that
$S \in \mathcal{I}$
such that
![]() $S_n\setminus S$
is finite for all
$S_n\setminus S$
is finite for all
![]() $n \in \textbf{N}$
. Lastly, we denote by
$n \in \textbf{N}$
. Lastly, we denote by
![]() $\mathcal{Z}$
the ideal of asymptotic density zero sets, i.e.,
$\mathcal{Z}$
the ideal of asymptotic density zero sets, i.e.,
where
![]() $\textsf{d}^\star(S) \;:\!=\; \limsup_n \frac{1}{n}\#(S\cap [1,n])$
stands for the upper asymptotic density of S, see e.g. [
Reference Leonetti and Tringali20
]. We refer to [
Reference Hrušák14
] for a recent survey on ideals and associated filters.
$\textsf{d}^\star(S) \;:\!=\; \limsup_n \frac{1}{n}\#(S\cap [1,n])$
stands for the upper asymptotic density of S, see e.g. [
Reference Leonetti and Tringali20
]. We refer to [
Reference Hrušák14
] for a recent survey on ideals and associated filters.
Let
![]() $x=(x_n)$
be a sequence taking values in a topological vector space X. Then we say that
$x=(x_n)$
be a sequence taking values in a topological vector space X. Then we say that
![]() $\eta \in X$
is an
$\eta \in X$
is an
![]() $\mathcal{I}$
-cluster point of x if
$\mathcal{I}$
-cluster point of x if
![]() $\{n \in \textbf{N}\;:\; x_n \in U\} \notin \mathcal{I}$
for all open neighbourhoods U of
$\{n \in \textbf{N}\;:\; x_n \in U\} \notin \mathcal{I}$
for all open neighbourhoods U of
![]() $\eta$
. Note that Fin-cluster points are the ordinary accumulation points. Usually
$\eta$
. Note that Fin-cluster points are the ordinary accumulation points. Usually
![]() $\mathcal{Z}$
-cluster points are referred to as statistical cluster points, see e.g. [
Reference Fridy13
]. It is worth noting that
$\mathcal{Z}$
-cluster points are referred to as statistical cluster points, see e.g. [
Reference Fridy13
]. It is worth noting that
![]() $\mathcal{I}$
-cluster points have been studied much before under a different name. Indeed, as it follows by [
Reference Leonetti and Maccheroni19
, theorem 4·2] and [
Reference Kadets and Seliutin16
, lemma 2·2], they correspond to classical “cluster points” of a filter (depending on x) on the underlying space, cf. [
Reference Bourbaki7
, definition 2, p.69].
$\mathcal{I}$
-cluster points have been studied much before under a different name. Indeed, as it follows by [
Reference Leonetti and Maccheroni19
, theorem 4·2] and [
Reference Kadets and Seliutin16
, lemma 2·2], they correspond to classical “cluster points” of a filter (depending on x) on the underlying space, cf. [
Reference Bourbaki7
, definition 2, p.69].
With these premises, for each
![]() $x \in (0,1]$
and for all integers
$x \in (0,1]$
and for all integers
![]() $b\ge 2$
and
$b\ge 2$
and
![]() $k\ge 1$
, let
$k\ge 1$
, let
![]() $\Gamma_b^k (x,\mathcal{I})$
be the set of
$\Gamma_b^k (x,\mathcal{I})$
be the set of
![]() $\mathcal{I}$
-cluster points of the sequence
$\mathcal{I}$
-cluster points of the sequence
![]() $({\boldsymbol{\pi}}_{b,n}^k(x)\;:\;n\ge 1)$
.
$({\boldsymbol{\pi}}_{b,n}^k(x)\;:\;n\ge 1)$
.
Theorem 2·1. The set
![]() $\{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I})=\Delta_{b}^k \text{ for all }b\ge 2,k\ge 1\}$
is comeager, provided that
$\{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I})=\Delta_{b}^k \text{ for all }b\ge 2,k\ge 1\}$
is comeager, provided that
![]() $\mathcal{I}$
is a meager ideal.
$\mathcal{I}$
is a meager ideal.
The class of meager ideals is really broad. Indeed, it contains Fin,
![]() $\mathcal{Z}$
, the summable ideal
$\mathcal{Z}$
, the summable ideal
![]() $\{S\subseteq \textbf{N}\;:\; \sum_{n \in S}1/n<\infty\}$
, the ideal generated by the upper Banach density, the analytic P-ideals, the Fubini sum
$\{S\subseteq \textbf{N}\;:\; \sum_{n \in S}1/n<\infty\}$
, the ideal generated by the upper Banach density, the analytic P-ideals, the Fubini sum
![]() $\textrm{Fin}\times \textrm{Fin}$
, the random graph ideal, etc.; cf. e.g. [
Reference Balcerzak, Leonetti and Głąb3, Reference Hrušák14
]. Note that
$\textrm{Fin}\times \textrm{Fin}$
, the random graph ideal, etc.; cf. e.g. [
Reference Balcerzak, Leonetti and Głąb3, Reference Hrušák14
]. Note that
![]() $\Gamma_b^k (x,\mathcal{I})=\textrm{L}_b^k(x)$
if
$\Gamma_b^k (x,\mathcal{I})=\textrm{L}_b^k(x)$
if
![]() $\mathcal{I}=\textrm{Fin}$
. Therefore Theorem 2·1 significantly strenghtens Theorem 1·1.
$\mathcal{I}=\textrm{Fin}$
. Therefore Theorem 2·1 significantly strenghtens Theorem 1·1.
Remark 2·2. It is not difficult to see that Theorem 2·1 does not hold without any restriction on
![]() $\mathcal{I}$
. Indeed, if
$\mathcal{I}$
. Indeed, if
![]() $\mathcal{I}$
is a maximal ideal (i.e., the complement of a free ultrafilter on
$\mathcal{I}$
is a maximal ideal (i.e., the complement of a free ultrafilter on
![]() $\textbf{N})$
, then for each
$\textbf{N})$
, then for each
![]() $x \in (0,1]$
and all integers
$x \in (0,1]$
and all integers
![]() $b\ge 2$
,
$b\ge 2$
,
![]() $k\ge 1$
, we have that the sequence
$k\ge 1$
, we have that the sequence
![]() $({\boldsymbol{\pi}}_{b,n}^k(x)\;:\;n\ge 1)$
is bounded, hence it is
$({\boldsymbol{\pi}}_{b,n}^k(x)\;:\;n\ge 1)$
is bounded, hence it is
![]() $\mathcal{I}$
-convergent so that
$\mathcal{I}$
-convergent so that
![]() $\Gamma_b^k (x,\mathcal{I})$
is a singleton.
$\Gamma_b^k (x,\mathcal{I})$
is a singleton.
On a similar direction, if
![]() $x=(x_n)$
is a sequence taking values in a topological vector space X, then
$x=(x_n)$
is a sequence taking values in a topological vector space X, then
![]() $\eta \in X$
is an
$\eta \in X$
is an
![]() $\mathcal{I}$
-limit point of x if there exists a subsequence
$\mathcal{I}$
-limit point of x if there exists a subsequence
![]() $(x_{n_k})$
such that
$(x_{n_k})$
such that
![]() $\lim_k x_{n_k}=\eta$
and
$\lim_k x_{n_k}=\eta$
and
![]() $\textbf{N}\setminus \{n_1,n_2,\ldots\} \in \mathcal{I}$
. Usually
$\textbf{N}\setminus \{n_1,n_2,\ldots\} \in \mathcal{I}$
. Usually
![]() $\mathcal{Z}$
-limit points are referred to as statistical limit points, see e.g. [
Reference Fridy13
]. Similarly, for each
$\mathcal{Z}$
-limit points are referred to as statistical limit points, see e.g. [
Reference Fridy13
]. Similarly, for each
![]() $x \in (0,1]$
and for all integers
$x \in (0,1]$
and for all integers
![]() $b\ge 2$
and
$b\ge 2$
and
![]() $k\ge 1$
, let
$k\ge 1$
, let
![]() $\Lambda_b^k (x,\mathcal{I})$
be the set of
$\Lambda_b^k (x,\mathcal{I})$
be the set of
![]() $\mathcal{I}$
-limit points of the sequence
$\mathcal{I}$
-limit points of the sequence
![]() $({\boldsymbol{\pi}}_{b,n}^k(x)\;:\;n\ge 1)$
. The analogue of Theorem 2·1 for
$({\boldsymbol{\pi}}_{b,n}^k(x)\;:\;n\ge 1)$
. The analogue of Theorem 2·1 for
![]() $\mathcal{I}$
-limit points follows.
$\mathcal{I}$
-limit points follows.
Theorem 2·3. The set
![]() $\{x \in (0,1]\;:\; \Lambda_b^k (x,\mathcal{I})=\Delta_{b}^k \text{ for all }b\ge 2,k\ge 1\}$
is comeager, provided that
$\{x \in (0,1]\;:\; \Lambda_b^k (x,\mathcal{I})=\Delta_{b}^k \text{ for all }b\ge 2,k\ge 1\}$
is comeager, provided that
![]() $\mathcal{I}$
is an analytic P-ideal or an
$\mathcal{I}$
is an analytic P-ideal or an
![]() $F_\sigma$
-ideal.
$F_\sigma$
-ideal.
It is known that every
![]() $\mathcal{I}$
-limit point is always an
$\mathcal{I}$
-limit point is always an
![]() $\mathcal{I}$
-cluster point, however they can be highly different, as it is shown in [
Reference Balcerzak and Leonetti2
, theorem 3·1]. This implies that Theorem 2·3 provides a further improvement on Theorem 2·1 for the subfamily of analytic P-ideals.
$\mathcal{I}$
-cluster point, however they can be highly different, as it is shown in [
Reference Balcerzak and Leonetti2
, theorem 3·1]. This implies that Theorem 2·3 provides a further improvement on Theorem 2·1 for the subfamily of analytic P-ideals.
It is remarkable that there exist
![]() $F_\sigma$
-ideals which are not P-ideals, see e.g. [
Reference Farah11
, section 1·11]. Also, the family of analytic P-ideals is well understood and has been characterised with the aid of lower semicontinuous submeasures, cf. Section 3. The results in [
Reference Borodulin-Nadzieja and Farkas6
] suggest that the study of the interplay between the theory of analytic P-ideals and their representability may have some relevant yet unexploited potential for the study of the geometry of Banach spaces.
$F_\sigma$
-ideals which are not P-ideals, see e.g. [
Reference Farah11
, section 1·11]. Also, the family of analytic P-ideals is well understood and has been characterised with the aid of lower semicontinuous submeasures, cf. Section 3. The results in [
Reference Borodulin-Nadzieja and Farkas6
] suggest that the study of the interplay between the theory of analytic P-ideals and their representability may have some relevant yet unexploited potential for the study of the geometry of Banach spaces.
Finally, recalling that the ideal
![]() $\mathcal{Z}$
defined in (2) is an analytic P-ideal, an immediate consequence of Theorem 2·3 (as pointed out in the abstract) follows:
$\mathcal{Z}$
defined in (2) is an analytic P-ideal, an immediate consequence of Theorem 2·3 (as pointed out in the abstract) follows:
Corollary 2·4. The set of
![]() $x \in (0,1]$
such that, for all
$x \in (0,1]$
such that, for all
![]() $b\ge 2$
and
$b\ge 2$
and
![]() $k\ge 1$
, every vector in
$k\ge 1$
, every vector in
![]() $\Delta_b^k$
is a statistical limit point of the sequence
$\Delta_b^k$
is a statistical limit point of the sequence
![]() $({\boldsymbol{\pi}}_{b,n}^k(x)\;:\; n\ge 1)$
is comeager.
$({\boldsymbol{\pi}}_{b,n}^k(x)\;:\; n\ge 1)$
is comeager.
It would also be interesting to investigate to what extend the same results for nonnormal points belonging to self-similar fractals (as studied, e.g., by Olsen and West in [ Reference Olsen and West24 ] in the context of iterated function systems) are valid.
We leave as open question for the interested reader to check whether Theorem 2·3 can be extended for all
![]() $F_{\sigma\delta}$
-ideals including, in particular, the ideal
$F_{\sigma\delta}$
-ideals including, in particular, the ideal
![]() $\mathcal{I}$
generated by the upper Banach density (which is known to not be a P-ideal, see e.g. [
Reference Freedman and Sember12
, p.299]).
$\mathcal{I}$
generated by the upper Banach density (which is known to not be a P-ideal, see e.g. [
Reference Freedman and Sember12
, p.299]).
3. Proofs of the main results
Proof of Theorem
2·1. Let
![]() $\mathcal{I}$
be a meager ideal on
$\mathcal{I}$
be a meager ideal on
![]() $\textbf{N}$
. It follows by Talagrand’s characterisation of meager ideals [
Reference Talagrand28
, theorem 21] that it is possible to define a partition
$\textbf{N}$
. It follows by Talagrand’s characterisation of meager ideals [
Reference Talagrand28
, theorem 21] that it is possible to define a partition
![]() $\{I_1,I_2,\ldots\}$
of
$\{I_1,I_2,\ldots\}$
of
![]() $\textbf{N}$
into nonempty finite subsets such that
$\textbf{N}$
into nonempty finite subsets such that
![]() $S\notin \mathcal{I}$
whenever
$S\notin \mathcal{I}$
whenever
![]() $I_n\subseteq S$
for infinitely many n. Moreover, we can assume without loss of generality that
$I_n\subseteq S$
for infinitely many n. Moreover, we can assume without loss of generality that
![]() $\max I_n<\min I_{n+1}$
for all
$\max I_n<\min I_{n+1}$
for all
![]() $n \in \textbf{N}$
.
$n \in \textbf{N}$
.
The claimed set can be rewritten as
![]() $\bigcap_{b\ge 2}\bigcap_{k\ge 1}X_b^k$
, where
$\bigcap_{b\ge 2}\bigcap_{k\ge 1}X_b^k$
, where
![]() $X_{b}^k \;:\!=\; \{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I})=\Delta_{b}^k\}$
. Since the family of meager subsets of (0,1] is a
$X_{b}^k \;:\!=\; \{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I})=\Delta_{b}^k\}$
. Since the family of meager subsets of (0,1] is a
![]() $\sigma$
-ideal, it is enough to show that the complement of each
$\sigma$
-ideal, it is enough to show that the complement of each
![]() $X_{b}^k$
is meager. To this aim, fix
$X_{b}^k$
is meager. To this aim, fix
![]() $b\ge 2$
and
$b\ge 2$
and
![]() $k\ge 1$
and denote by
$k\ge 1$
and denote by
![]() $\|\!\cdot\! \|$
the Euclidean norm on
$\|\!\cdot\! \|$
the Euclidean norm on
![]() $\textbf{R}^{b^k}$
. Considering that
$\textbf{R}^{b^k}$
. Considering that
![]() $\{{\boldsymbol{\eta}}_1, {\boldsymbol{\eta}}_2, \ldots\} \;:\!=\; \Delta_b^k \cap \textbf{Q}^{b^k}$
is a countable dense subset of
$\{{\boldsymbol{\eta}}_1, {\boldsymbol{\eta}}_2, \ldots\} \;:\!=\; \Delta_b^k \cap \textbf{Q}^{b^k}$
is a countable dense subset of
![]() $\Delta_b^k$
and that
$\Delta_b^k$
and that
![]() $\Gamma_b^k(x,\mathcal{I})$
is a closed subset of
$\Gamma_b^k(x,\mathcal{I})$
is a closed subset of
![]() $\Delta_b^k$
by [
Reference Leonetti and Maccheroni19
, lemma 3·1(iv)], it follows that
$\Delta_b^k$
by [
Reference Leonetti and Maccheroni19
, lemma 3·1(iv)], it follows that
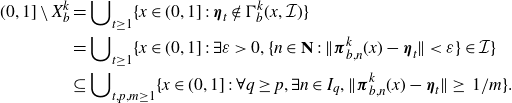 \begin{equation*}\begin{split}(0,1]\setminus X_b^k&= \bigcup\nolimits_{t\ge 1}\{x \in (0,1]\;:\; {\boldsymbol{\eta}}_t \notin \Gamma_b^k(x, \mathcal{I})\}\\&= \bigcup\nolimits_{t\ge 1}\{x \in (0,1]\;:\; \exists \varepsilon>0, \{n \in \textbf{N}\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}_t\|< \varepsilon\}\in \mathcal{I}\}\\&\subseteq \bigcup\nolimits_{t, p, m\ge 1}\{x \in (0,1]\;:\; \forall q\ge p, \exists n \in I_q, \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}_t\|\ge\; {1}/{m} \}.\\\end{split}\end{equation*}
\begin{equation*}\begin{split}(0,1]\setminus X_b^k&= \bigcup\nolimits_{t\ge 1}\{x \in (0,1]\;:\; {\boldsymbol{\eta}}_t \notin \Gamma_b^k(x, \mathcal{I})\}\\&= \bigcup\nolimits_{t\ge 1}\{x \in (0,1]\;:\; \exists \varepsilon>0, \{n \in \textbf{N}\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}_t\|< \varepsilon\}\in \mathcal{I}\}\\&\subseteq \bigcup\nolimits_{t, p, m\ge 1}\{x \in (0,1]\;:\; \forall q\ge p, \exists n \in I_q, \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}_t\|\ge\; {1}/{m} \}.\\\end{split}\end{equation*}
Denote by
![]() $S_{t,m,p}$
the set in the latter union. Thus it is sufficient to show that each
$S_{t,m,p}$
the set in the latter union. Thus it is sufficient to show that each
![]() $S_{t,p,m}$
is nowhere dense. To this aim, fix
$S_{t,p,m}$
is nowhere dense. To this aim, fix
![]() $t,p,m \in \textbf{N}$
and a nonempty relatively open set
$t,p,m \in \textbf{N}$
and a nonempty relatively open set
![]() $G\subseteq (0,1]$
. We claim there exists a nonempty open set U contained in G and disjoint from
$G\subseteq (0,1]$
. We claim there exists a nonempty open set U contained in G and disjoint from
![]() $S_{t,p,m}$
. Since G is nonempty and open in (0, 1], there exists a string
$S_{t,p,m}$
. Since G is nonempty and open in (0, 1], there exists a string
![]() $\tilde{{\boldsymbol{s}}}=s_1\cdots s_j \in S_b^j$
such that
$\tilde{{\boldsymbol{s}}}=s_1\cdots s_j \in S_b^j$
such that
![]() $x \in G$
whenever
$x \in G$
whenever
![]() $d_{b,i}(x)=s_i$
for all
$d_{b,i}(x)=s_i$
for all
![]() $i=1,\ldots,j$
. Now, pick
$i=1,\ldots,j$
. Now, pick
![]() $x^\star \in (0,1]$
such that
$x^\star \in (0,1]$
such that
![]() $\lim_n {\boldsymbol{\pi}}_{b,n}^k(x^\star)={\boldsymbol{\eta}}_t$
, which exists by [
Reference Olsen22
, theorem 1]. In addition, we can assume without loss of generality that
$\lim_n {\boldsymbol{\pi}}_{b,n}^k(x^\star)={\boldsymbol{\eta}}_t$
, which exists by [
Reference Olsen22
, theorem 1]. In addition, we can assume without loss of generality that
![]() $d_{b,i}(x^\star)=s_i$
for all
$d_{b,i}(x^\star)=s_i$
for all
![]() $i=1,\ldots,j$
. Since
$i=1,\ldots,j$
. Since
![]() ${\boldsymbol{\pi}}_{b,n}^k(x^\star)$
is convergent to
${\boldsymbol{\pi}}_{b,n}^k(x^\star)$
is convergent to
![]() ${\boldsymbol{\eta}}_t$
, there exists
${\boldsymbol{\eta}}_t$
, there exists
![]() $q \ge p+j$
such that
$q \ge p+j$
such that
![]() $\|{\boldsymbol{\pi}}^k_{b,n}(x^\star)-{\boldsymbol{\eta}}_{t} \|< \;{1}/{m}$
for all
$\|{\boldsymbol{\pi}}^k_{b,n}(x^\star)-{\boldsymbol{\eta}}_{t} \|< \;{1}/{m}$
for all
![]() $n \ge \min I_{q}$
. Define
$n \ge \min I_{q}$
. Define
![]() $V \;:\!=\; \{x \in (0,1]\;:\; d_{b,i}(x)=d_{b,i}(x^\star) \text{ for all }i=1,\ldots,\max I_{q}+k\}$
and note that
$V \;:\!=\; \{x \in (0,1]\;:\; d_{b,i}(x)=d_{b,i}(x^\star) \text{ for all }i=1,\ldots,\max I_{q}+k\}$
and note that
![]() $V\subseteq G$
because
$V\subseteq G$
because
![]() $d_{b,i}(x)=s_i$
for all
$d_{b,i}(x)=s_i$
for all
![]() $i\le j$
and
$i\le j$
and
![]() $x \in V$
, and
$x \in V$
, and
![]() $V\cap S_{t,m,p}=\emptyset$
because, for each
$V\cap S_{t,m,p}=\emptyset$
because, for each
![]() $x\in V$
, the required property is not satisfied for this choice of q since
$x\in V$
, the required property is not satisfied for this choice of q since
![]() ${\boldsymbol{\pi}}_{b,n}^k(x)={\boldsymbol{\pi}}_{b,n}^k(x^\star)$
for all
${\boldsymbol{\pi}}_{b,n}^k(x)={\boldsymbol{\pi}}_{b,n}^k(x^\star)$
for all
![]() $n \le \max I_q$
. Clearly, V has nonempty interior, hence it is possible to choose such
$n \le \max I_q$
. Clearly, V has nonempty interior, hence it is possible to choose such
![]() $U\subseteq V$
.
$U\subseteq V$
.
This proves that each
![]() $S_{t,m,p}$
is nowhere dense, concluding the proof.
$S_{t,m,p}$
is nowhere dense, concluding the proof.
Before we proceed to the proof of Theorem 2·3, we need to recall the classical Solecki’s characterisation of analytic P-ideals. A lower semicontinuous submeasure (in short, lscsm) is a monotone subadditive function
![]() $\varphi\;:\; \mathcal{P}(\textbf{N}) \to [0,\infty]$
such that
$\varphi\;:\; \mathcal{P}(\textbf{N}) \to [0,\infty]$
such that
![]() $\varphi(\emptyset)=0$
,
$\varphi(\emptyset)=0$
,
![]() $\varphi(\{n\})<\infty$
, and
$\varphi(\{n\})<\infty$
, and
![]() $\varphi(A)=\lim_m \varphi(A\cap [1,m])$
for all
$\varphi(A)=\lim_m \varphi(A\cap [1,m])$
for all
![]() $A\subseteq \textbf{N}$
and
$A\subseteq \textbf{N}$
and
![]() $n \in \textbf{N}$
. It follows by [
Reference Solecki26
, theorem 3·1] that an ideal
$n \in \textbf{N}$
. It follows by [
Reference Solecki26
, theorem 3·1] that an ideal
![]() $\mathcal{I}$
is an analytic P-ideal if and only if there exists a lscsm
$\mathcal{I}$
is an analytic P-ideal if and only if there exists a lscsm
![]() $\varphi$
such that
$\varphi$
such that
Here,
![]() $\|A\|_\varphi \;:\!=\; \lim_n \varphi(A\setminus [1,n])$
for all
$\|A\|_\varphi \;:\!=\; \lim_n \varphi(A\setminus [1,n])$
for all
![]() $A\subseteq \textbf{N}$
. Note that
$A\subseteq \textbf{N}$
. Note that
![]() $\|A\|_\varphi=\|B\|_\varphi$
whenever the symmetric difference
$\|A\|_\varphi=\|B\|_\varphi$
whenever the symmetric difference
![]() $A\bigtriangleup B$
is finite, cf. [
Reference Farah11
, lemma 1·3·3(b)]. Easy examples of lscsms are
$A\bigtriangleup B$
is finite, cf. [
Reference Farah11
, lemma 1·3·3(b)]. Easy examples of lscsms are
![]() $\varphi(A) \;:\!=\; \# A$
or
$\varphi(A) \;:\!=\; \# A$
or
![]() $\varphi(A) \;:\!=\; \sup_n \!({1}/{n})\#(A \cap [1,n])$
for all
$\varphi(A) \;:\!=\; \sup_n \!({1}/{n})\#(A \cap [1,n])$
for all
![]() $A\subseteq \textbf{N}$
which lead, respectively, to the ideals Fin and
$A\subseteq \textbf{N}$
which lead, respectively, to the ideals Fin and
![]() $\mathcal{Z}$
through the representation (3).
$\mathcal{Z}$
through the representation (3).
Proof of Theorem
2·3. First, let us suppose that
![]() $\mathcal{I}$
is an
$\mathcal{I}$
is an
![]() $F_\sigma$
-ideal. We obtain by [
Reference Balcerzak and Leonetti2
, theorem 2·3] that
$F_\sigma$
-ideal. We obtain by [
Reference Balcerzak and Leonetti2
, theorem 2·3] that
![]() $\Lambda_b^k (x,\mathcal{I})=\Gamma_b^k (x,\mathcal{I})$
for each
$\Lambda_b^k (x,\mathcal{I})=\Gamma_b^k (x,\mathcal{I})$
for each
![]() $b\ge 2$
,
$b\ge 2$
,
![]() $k\ge 1$
, and
$k\ge 1$
, and
![]() $x \in (0,1]$
. Therefore the claim follows by Theorem 2·1.
$x \in (0,1]$
. Therefore the claim follows by Theorem 2·1.
Then, we assume hereafter that
![]() $\mathcal{I}$
is an analytic P-ideal generated by a lscsm
$\mathcal{I}$
is an analytic P-ideal generated by a lscsm
![]() $\varphi$
as in (3). Fix integers
$\varphi$
as in (3). Fix integers
![]() $b\ge 2$
and
$b\ge 2$
and
![]() $k\ge 1$
, and define the function
$k\ge 1$
, and define the function
where
![]() $\|\!\cdot\!\|$
stands for the Euclidean norm on
$\|\!\cdot\!\|$
stands for the Euclidean norm on
![]() $\textbf{R}^{b^k}$
. It follows by [
Reference Balcerzak and Leonetti2
, lemma 2·1] that every section
$\textbf{R}^{b^k}$
. It follows by [
Reference Balcerzak and Leonetti2
, lemma 2·1] that every section
![]() $\mathfrak{u}(x,\cdot)$
is upper semicontinuous, so that the set
$\mathfrak{u}(x,\cdot)$
is upper semicontinuous, so that the set
is closed for each
![]() $x \in (0,1]$
and
$x \in (0,1]$
and
![]() $q \in \textbf{R}$
.
$q \in \textbf{R}$
.
At this point, we prove that, for each
![]() ${\boldsymbol{\eta}} \in \Delta_b^k$
, the set
${\boldsymbol{\eta}} \in \Delta_b^k$
, the set
![]() $X({\boldsymbol{\eta}}) \;:\!=\; \{x \in (0,1]\;:\; \mathfrak{u}(x,{\boldsymbol{\eta}}) \ge\; {1}/{2}\}$
is comeager. To this aim, fix
$X({\boldsymbol{\eta}}) \;:\!=\; \{x \in (0,1]\;:\; \mathfrak{u}(x,{\boldsymbol{\eta}}) \ge\; {1}/{2}\}$
is comeager. To this aim, fix
![]() ${\boldsymbol{\eta}} \in \Delta_b^k$
and notice that
${\boldsymbol{\eta}} \in \Delta_b^k$
and notice that
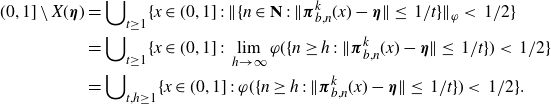 \begin{equation*}\begin{split}(0,1]\setminus X({\boldsymbol{\eta}})&=\bigcup\nolimits_{t\ge 1}\{x \in (0,1]\;:\; \|\{n \in \textbf{N}\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le\; {1}/{t}\}\|_\varphi < \; {1}/{2}\}\\&=\bigcup\nolimits_{t\ge 1}\{x \in (0,1]\;:\; \lim_{h\to \infty} \varphi(\{n\ge h\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le\; {1}/{t}\})< \; {1}/{2}\}\\&=\bigcup\nolimits_{t,h\ge 1}\{x \in (0,1]\;:\; \varphi(\{n\ge h \;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le \; {1}/{t}\})< \; {1}/{2}\}.\end{split}\end{equation*}
\begin{equation*}\begin{split}(0,1]\setminus X({\boldsymbol{\eta}})&=\bigcup\nolimits_{t\ge 1}\{x \in (0,1]\;:\; \|\{n \in \textbf{N}\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le\; {1}/{t}\}\|_\varphi < \; {1}/{2}\}\\&=\bigcup\nolimits_{t\ge 1}\{x \in (0,1]\;:\; \lim_{h\to \infty} \varphi(\{n\ge h\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le\; {1}/{t}\})< \; {1}/{2}\}\\&=\bigcup\nolimits_{t,h\ge 1}\{x \in (0,1]\;:\; \varphi(\{n\ge h \;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le \; {1}/{t}\})< \; {1}/{2}\}.\end{split}\end{equation*}
Denoting by
![]() $Y_{t,h}$
the inner set above, it is sufficient to show that each
$Y_{t,h}$
the inner set above, it is sufficient to show that each
![]() $Y_{t,h}$
is nowhere dense. Hence, fix
$Y_{t,h}$
is nowhere dense. Hence, fix
![]() $G\subseteq (0,1]$
,
$G\subseteq (0,1]$
,
![]() $\tilde{{\boldsymbol{s}}} \in S_b^j$
, and
$\tilde{{\boldsymbol{s}}} \in S_b^j$
, and
![]() $x^\star \in (0,1]$
as in the proof of Theorem 2·1. Considering that
$x^\star \in (0,1]$
as in the proof of Theorem 2·1. Considering that
![]() $\|\!\cdot\!\|_\varphi$
is invariant under finite sets, it follows that
$\|\!\cdot\!\|_\varphi$
is invariant under finite sets, it follows that
where
![]() $j^\prime \;:\!=\; j+h$
. Since
$j^\prime \;:\!=\; j+h$
. Since
![]() $\varphi$
is lower semicontinuous, there exists an integer
$\varphi$
is lower semicontinuous, there exists an integer
![]() $j^{\prime\prime}>j^\prime$
such that
$j^{\prime\prime}>j^\prime$
such that
Define
![]() $V \;:\!=\; \{x \in (0,1]\;:\; d_{b,i}(x)=d_{b,i}(x^\star) \text{ for all }i=1,\ldots,j^{\prime\prime}\}$
. Similarly, note that
$V \;:\!=\; \{x \in (0,1]\;:\; d_{b,i}(x)=d_{b,i}(x^\star) \text{ for all }i=1,\ldots,j^{\prime\prime}\}$
. Similarly, note that
![]() $V\subseteq G$
because
$V\subseteq G$
because
![]() $d_{b,i}(x)=s_i$
for all
$d_{b,i}(x)=s_i$
for all
![]() $i\le j$
and
$i\le j$
and
![]() $x \in V$
, and
$x \in V$
, and
![]() $V \cap Y_{t,h}=\emptyset$
because
$V \cap Y_{t,h}=\emptyset$
because
![]() $\varphi(\{n\ge h\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le\; {1}/{t}\})$
is at least
$\varphi(\{n\ge h\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le\; {1}/{t}\})$
is at least
![]() $\varphi(\{n\in [j^\prime, j^{\prime\prime}]\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le\; {1}/{t}\})\ge \; {1}/{2}$
for all
$\varphi(\{n\in [j^\prime, j^{\prime\prime}]\;:\; \|{\boldsymbol{\pi}}_{b,n}^k(x)-{\boldsymbol{\eta}}\|\le\; {1}/{t}\})\ge \; {1}/{2}$
for all
![]() $x \in V$
. Since V has nonempty interior, it is possible to choose
$x \in V$
. Since V has nonempty interior, it is possible to choose
![]() $U\subseteq V$
with the required property.
$U\subseteq V$
with the required property.
Finally, let E be a countable dense subset of
![]() $\Delta_b^k$
. Considering that
$\Delta_b^k$
. Considering that
![]() $X \;:\!=\; \{x \in (0,1]\;:\; E\subseteq \Lambda_b^k(x,\mathcal{I},\; {1}/{2})\}$
is equal to
$X \;:\!=\; \{x \in (0,1]\;:\; E\subseteq \Lambda_b^k(x,\mathcal{I},\; {1}/{2})\}$
is equal to
![]() $\bigcap_{{\boldsymbol{\eta}} \in E}X({\boldsymbol{\eta}})$
, it follows that the set
$\bigcap_{{\boldsymbol{\eta}} \in E}X({\boldsymbol{\eta}})$
, it follows that the set
![]() $X$
is comeager. However, considering that
$X$
is comeager. However, considering that
by [
Reference Balcerzak and Leonetti2
, theorem 2·2] and that
![]() $\Lambda_b^k(x,\mathcal{I},\; {1}/{2})$
is a closed subset such that
$\Lambda_b^k(x,\mathcal{I},\; {1}/{2})$
is a closed subset such that
![]() $E\subseteq \Lambda_b^k(x,\mathcal{I},\; {1}/{2})\subseteq \Lambda_b^k(x,\mathcal{I})\subseteq \Delta_b^k$
for all
$E\subseteq \Lambda_b^k(x,\mathcal{I},\; {1}/{2})\subseteq \Lambda_b^k(x,\mathcal{I})\subseteq \Delta_b^k$
for all
![]() $x \in X$
, we obtain that
$x \in X$
, we obtain that
![]() $\Lambda_b^k(x,\mathcal{I}, \; {1}/{2})=\Lambda_b^k(x,\mathcal{I})=\Delta_b^k$
for all
$\Lambda_b^k(x,\mathcal{I}, \; {1}/{2})=\Lambda_b^k(x,\mathcal{I})=\Delta_b^k$
for all
![]() $x \in X$
. In particular, the claimed set contains X, which is comeager. This concludes the proof.
$x \in X$
. In particular, the claimed set contains X, which is comeager. This concludes the proof.
4. Applications
4·1. Hausdorff and packing dimensions
We refer to [ Reference Falconer10 , chapter 3] for the definitions of the Hausdorff dimension and the packing dimension.
Proposition 4·1. The sets defined in Theorem 2·1 and Theorem 2·3 have Hausdorff dimension 0 and packing dimension 1.
Proof. Reasoning as in [ Reference Olsen23 ], the claimed sets are contained in the corresponding ones with ideal Fin, which have Hausdorff dimension 0 by [ Reference Olsen22 , theorem 2·1]. In addition, since all sets are comeager, we conclude that they have packing dimension 1 by [ Reference Falconer10 , corollary 3·10(b)].
4·2. Regular matrices
We extend the main results contained in [
Reference Hyde, Laschos, Olsen, Petrykiewicz and Shaw15, Reference Stylianou27
]. To this aim, let
![]() $A=(a_{n,i}\;:\; n,i \in \textbf{N})$
be a regular matrix, that is, an infinite real-valued matrix such that, if
$A=(a_{n,i}\;:\; n,i \in \textbf{N})$
be a regular matrix, that is, an infinite real-valued matrix such that, if
![]() ${\boldsymbol{z}}=({\boldsymbol{z}}_n)$
is a
${\boldsymbol{z}}=({\boldsymbol{z}}_n)$
is a
![]() $\textbf{R}^d$
-valued sequence convergent to
$\textbf{R}^d$
-valued sequence convergent to
![]() ${\boldsymbol{\eta}}$
, then
${\boldsymbol{\eta}}$
, then
![]() $A_n{\boldsymbol{z}} \;:\!=\; \sum_i a_{n,i}{\boldsymbol{z}}_i$
exists for all
$A_n{\boldsymbol{z}} \;:\!=\; \sum_i a_{n,i}{\boldsymbol{z}}_i$
exists for all
![]() $n \in \textbf{N}$
and
$n \in \textbf{N}$
and
![]() $\lim_n A_n{\boldsymbol{z}}={\boldsymbol{\eta}}$
, see e.g. [
Reference Cooke9
, chapter 4]. Then, for each
$\lim_n A_n{\boldsymbol{z}}={\boldsymbol{\eta}}$
, see e.g. [
Reference Cooke9
, chapter 4]. Then, for each
![]() $x \in (0,1]$
and integers
$x \in (0,1]$
and integers
![]() $b\ge 2$
and
$b\ge 2$
and
![]() $k\ge 1$
, let
$k\ge 1$
, let
![]() $\Gamma_{b}^k(x,\mathcal{I},A)$
be the set of
$\Gamma_{b}^k(x,\mathcal{I},A)$
be the set of
![]() $\mathcal{I}$
-cluster points of the sequence of vectors
$\mathcal{I}$
-cluster points of the sequence of vectors
![]() $\left(A_n{\boldsymbol{\pi}}_{b}^k(x)\;:\; n \ge 1\right)$
, where
$\left(A_n{\boldsymbol{\pi}}_{b}^k(x)\;:\; n \ge 1\right)$
, where
![]() ${\boldsymbol{\pi}}_{b}^k(x)$
is the sequence
${\boldsymbol{\pi}}_{b}^k(x)$
is the sequence
![]() $({\boldsymbol{\pi}}_{b,n}^k(x)\;:\; n\ge 1)$
.
$({\boldsymbol{\pi}}_{b,n}^k(x)\;:\; n\ge 1)$
.
In particular,
![]() $\Gamma_{b}^k(x,\mathcal{I},A)=\Gamma_{b}^k(x,\mathcal{I})$
if A is the infinite identity matrix.
$\Gamma_{b}^k(x,\mathcal{I},A)=\Gamma_{b}^k(x,\mathcal{I})$
if A is the infinite identity matrix.
Theorem 4·2. The set
![]() $\{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I},A)\supseteq \Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager, provided that
$\{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I},A)\supseteq \Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager, provided that
![]() $\mathcal{I}$
is a meager ideal and A is a regular matrix.
$\mathcal{I}$
is a meager ideal and A is a regular matrix.
Proof. Fix a regular matrix
![]() $A=(a_{n,i})$
and a meager ideal
$A=(a_{n,i})$
and a meager ideal
![]() $\mathcal{I}$
. The proof goes along the same lines as the proof of Theorem 2·1, replacing the definition of
$\mathcal{I}$
. The proof goes along the same lines as the proof of Theorem 2·1, replacing the definition of
![]() $S_{t,m,p}$
with
$S_{t,m,p}$
with
Recall that, thanks to the classical Silverman–Toeplitz characterisation of regular matrices, see e.g. [
Reference Cooke9
, theorem 4·1, II] or [
Reference Connor and Leonetti8
], we have that
![]() $\sup_n \sum_i |a_{n,i}|<\infty$
. Since
$\sup_n \sum_i |a_{n,i}|<\infty$
. Since
![]() $\lim_n {\boldsymbol{\pi}}_{b,n}^k(x^\star)={\boldsymbol{\eta}}_t$
, it follows that there exist sufficiently large integers
$\lim_n {\boldsymbol{\pi}}_{b,n}^k(x^\star)={\boldsymbol{\eta}}_t$
, it follows that there exist sufficiently large integers
![]() $q\ge p+j$
and
$q\ge p+j$
and
![]() $j_A \ge j$
such that, if
$j_A \ge j$
such that, if
![]() $d_{b,i}(x)=d_{b,i}(x^\star)$
for all
$d_{b,i}(x)=d_{b,i}(x^\star)$
for all
![]() $i=1,\ldots,j_A+k$
, then
$i=1,\ldots,j_A+k$
, then
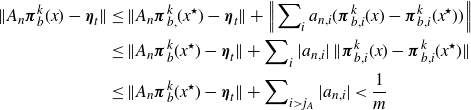 \begin{equation}\begin{split}\|A_n{\boldsymbol{\pi}}^k_{b}(x)-{\boldsymbol{\eta}}_{t} \|&\le \|A_n{\boldsymbol{\pi}}^k_{b, }(x^\star)-{\boldsymbol{\eta}}_{t}\|+\left\|\sum\nolimits_i a_{n,i}({\boldsymbol{\pi}}^k_{b,i}(x)-{\boldsymbol{\pi}}^k_{b,i}(x^\star))\right\|\\&\le \|A_n{\boldsymbol{\pi}}^k_{b }(x^\star)-{\boldsymbol{\eta}}_{t} \|+\sum\nolimits_i |a_{n,i}| \, \|{\boldsymbol{\pi}}^k_{b,i}(x)-{\boldsymbol{\pi}}^k_{b,i}(x^\star)\|\\&\le \|A_n{\boldsymbol{\pi}}^k_{b}(x^\star)-{\boldsymbol{\eta}}_{t}\|+\sum\nolimits_{i> j_A} |a_{n,i}|< \frac{1}{m}\end{split}\end{equation}
\begin{equation}\begin{split}\|A_n{\boldsymbol{\pi}}^k_{b}(x)-{\boldsymbol{\eta}}_{t} \|&\le \|A_n{\boldsymbol{\pi}}^k_{b, }(x^\star)-{\boldsymbol{\eta}}_{t}\|+\left\|\sum\nolimits_i a_{n,i}({\boldsymbol{\pi}}^k_{b,i}(x)-{\boldsymbol{\pi}}^k_{b,i}(x^\star))\right\|\\&\le \|A_n{\boldsymbol{\pi}}^k_{b }(x^\star)-{\boldsymbol{\eta}}_{t} \|+\sum\nolimits_i |a_{n,i}| \, \|{\boldsymbol{\pi}}^k_{b,i}(x)-{\boldsymbol{\pi}}^k_{b,i}(x^\star)\|\\&\le \|A_n{\boldsymbol{\pi}}^k_{b}(x^\star)-{\boldsymbol{\eta}}_{t}\|+\sum\nolimits_{i> j_A} |a_{n,i}|< \frac{1}{m}\end{split}\end{equation}
for all
![]() $n \in I_{q}$
. We conclude analogously that
$n \in I_{q}$
. We conclude analogously that
![]() $S^\prime_{t,m,p}$
is nowhere dense.
$S^\prime_{t,m,p}$
is nowhere dense.
The main result in [
Reference Stylianou27
] corresponds to the case
![]() $\mathcal{I}=\textrm{Fin}$
and
$\mathcal{I}=\textrm{Fin}$
and
![]() $k=1$
, although with a different proof; cf. also Example 4·10 below.
$k=1$
, although with a different proof; cf. also Example 4·10 below.
At this point, we need an intermediate result which is of independent interest. For each bounded sequence
![]() ${\boldsymbol{x}}=({\boldsymbol{x}}_n)$
with values in
${\boldsymbol{x}}=({\boldsymbol{x}}_n)$
with values in
![]() $\textbf{R}^k$
, let
$\textbf{R}^k$
, let
![]() $\textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})$
be the Knopp core of
$\textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})$
be the Knopp core of
![]() ${\boldsymbol{x}}$
, that is, the convex hull of the set of accumulation points of
${\boldsymbol{x}}$
, that is, the convex hull of the set of accumulation points of
![]() ${\boldsymbol{x}}$
. In other words,
${\boldsymbol{x}}$
. In other words,
![]() $\textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})=\textrm{co}\, \textrm{L}_{{\boldsymbol{x}}}$
, where
$\textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})=\textrm{co}\, \textrm{L}_{{\boldsymbol{x}}}$
, where
![]() $\textrm{co}\, S$
is the convex hull of
$\textrm{co}\, S$
is the convex hull of
![]() $S\subseteq \textbf{R}^k$
and
$S\subseteq \textbf{R}^k$
and
![]() $\textrm{L}_{{\boldsymbol{x}}}$
is the set of accumulation points of
$\textrm{L}_{{\boldsymbol{x}}}$
is the set of accumulation points of
![]() ${\boldsymbol{x}}$
. The ideal version of the Knopp core has been studied in [
Reference Kadets and Seliutin16, Reference Leonetti18
]. The classical Knopp theorem states that, if
${\boldsymbol{x}}$
. The ideal version of the Knopp core has been studied in [
Reference Kadets and Seliutin16, Reference Leonetti18
]. The classical Knopp theorem states that, if
![]() $k=2$
and A is a nonnegative regular matrix, then
$k=2$
and A is a nonnegative regular matrix, then
for all bounded sequences
![]() ${\boldsymbol{x}}$
, where
${\boldsymbol{x}}$
, where
![]() $A{\boldsymbol{x}}=(A_n{\boldsymbol{x}}\;:\; n\ge 1)$
, see [
Reference Knopp17
, p. 115]; cf. [
Reference Cooke9
, chapter 6] for a textbook exposition. A generalisation in the case
$A{\boldsymbol{x}}=(A_n{\boldsymbol{x}}\;:\; n\ge 1)$
, see [
Reference Knopp17
, p. 115]; cf. [
Reference Cooke9
, chapter 6] for a textbook exposition. A generalisation in the case
![]() $k=1$
can be found in [
Reference Maddox21
]. We show, in particular, that a stronger version of Knopp’s theorem holds for every
$k=1$
can be found in [
Reference Maddox21
]. We show, in particular, that a stronger version of Knopp’s theorem holds for every
![]() $k \in \textbf{N}$
.
$k \in \textbf{N}$
.
Proposition 4·3. Let
![]() ${\boldsymbol{x}}=({\boldsymbol{x}}_n)$
be a bounded sequence taking values in
${\boldsymbol{x}}=({\boldsymbol{x}}_n)$
be a bounded sequence taking values in
![]() $\mathbf{R}^k$
, and fix a regular matrix A such that
$\mathbf{R}^k$
, and fix a regular matrix A such that
![]() $\lim_n \sum_i |a_{n,i}|=1$
. Then inclusion (5) holds.
$\lim_n \sum_i |a_{n,i}|=1$
. Then inclusion (5) holds.
Proof. Define
![]() $\kappa \;:\!=\; \sup_n \|{\boldsymbol{x}}_n\|$
and let
$\kappa \;:\!=\; \sup_n \|{\boldsymbol{x}}_n\|$
and let
![]() ${\boldsymbol{\eta}}$
be an accumulation point of
${\boldsymbol{\eta}}$
be an accumulation point of
![]() $A{\boldsymbol{x}}$
. It is sufficient to show that
$A{\boldsymbol{x}}$
. It is sufficient to show that
![]() ${\boldsymbol{\eta}}\in K \;:\!=\; \textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})$
. Possibly deleting some rows of A, we can assume without loss of generality that
${\boldsymbol{\eta}}\in K \;:\!=\; \textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})$
. Possibly deleting some rows of A, we can assume without loss of generality that
![]() $\lim A{\boldsymbol{x}}={\boldsymbol{\eta}}$
. For each
$\lim A{\boldsymbol{x}}={\boldsymbol{\eta}}$
. For each
![]() $m \in \textbf{N}$
, let
$m \in \textbf{N}$
, let
![]() $K_m$
be the closure of
$K_m$
be the closure of
![]() $\textrm{co}\{x_m,x_{m+1},\ldots\}$
, hence
$\textrm{co}\{x_m,x_{m+1},\ldots\}$
, hence
![]() $K\subseteq K_m$
. Define
$K\subseteq K_m$
. Define
![]() $d({\boldsymbol{a}}, C) \;:\!=\; \min_{{\boldsymbol{b}} \in C} \|{\boldsymbol{a}}-{\boldsymbol{b}}\|$
for all
$d({\boldsymbol{a}}, C) \;:\!=\; \min_{{\boldsymbol{b}} \in C} \|{\boldsymbol{a}}-{\boldsymbol{b}}\|$
for all
![]() ${\boldsymbol{a}} \in \textbf{R}^k$
and nonempty compact sets
${\boldsymbol{a}} \in \textbf{R}^k$
and nonempty compact sets
![]() $C\subseteq \textbf{R}^k$
. In addition, for each
$C\subseteq \textbf{R}^k$
. In addition, for each
![]() $m \in \textbf{N}$
, let
$m \in \textbf{N}$
, let
![]() $Q_m({\boldsymbol{a}})\in K_m$
be the unique vector such that
$Q_m({\boldsymbol{a}})\in K_m$
be the unique vector such that
![]() $d({\boldsymbol{a}}, K_m)=\|{\boldsymbol{a}}-Q_m({\boldsymbol{a}})\|$
. Similarly, let
$d({\boldsymbol{a}}, K_m)=\|{\boldsymbol{a}}-Q_m({\boldsymbol{a}})\|$
. Similarly, let
![]() $Q({\boldsymbol{a}})$
be the vector in K which minimizes its distance with
$Q({\boldsymbol{a}})$
be the vector in K which minimizes its distance with
![]() ${\boldsymbol{a}}$
. Then, notice that, for all
${\boldsymbol{a}}$
. Then, notice that, for all
![]() $n,m \in \textbf{N}$
, we have
$n,m \in \textbf{N}$
, we have
 \begin{equation*}\begin{split}d(A_n{\boldsymbol{x}}, K) &\le \inf\nolimits_{{\boldsymbol{b}} \in K} \inf\nolimits_{{\boldsymbol{c}} \in \textbf{R}^k} (\|A_n{\boldsymbol{x}}-{\boldsymbol{c}}\|+\|{\boldsymbol{c}}-{\boldsymbol{b}}\|) \\&\le \inf\nolimits_{{\boldsymbol{c}} \in K_m} \inf\nolimits_{{\boldsymbol{b}} \in K} (\|A_n{\boldsymbol{x}}-{\boldsymbol{c}}\|+\|{\boldsymbol{c}}-{\boldsymbol{b}}\|) \\&\le \inf\nolimits_{{\boldsymbol{c}} \in K_m} \|A_n{\boldsymbol{x}}-{\boldsymbol{c}}\|+\sup\nolimits_{{\boldsymbol{y}}\in K_m} \inf\nolimits_{{\boldsymbol{b}} \in K}\|{\boldsymbol{y}}-{\boldsymbol{b}}\| \\&= d(A_n{\boldsymbol{x}},K_m)+\sup\nolimits_{{\boldsymbol{y}}\in K_m}d({\boldsymbol{y}},K).\end{split}\end{equation*}
\begin{equation*}\begin{split}d(A_n{\boldsymbol{x}}, K) &\le \inf\nolimits_{{\boldsymbol{b}} \in K} \inf\nolimits_{{\boldsymbol{c}} \in \textbf{R}^k} (\|A_n{\boldsymbol{x}}-{\boldsymbol{c}}\|+\|{\boldsymbol{c}}-{\boldsymbol{b}}\|) \\&\le \inf\nolimits_{{\boldsymbol{c}} \in K_m} \inf\nolimits_{{\boldsymbol{b}} \in K} (\|A_n{\boldsymbol{x}}-{\boldsymbol{c}}\|+\|{\boldsymbol{c}}-{\boldsymbol{b}}\|) \\&\le \inf\nolimits_{{\boldsymbol{c}} \in K_m} \|A_n{\boldsymbol{x}}-{\boldsymbol{c}}\|+\sup\nolimits_{{\boldsymbol{y}}\in K_m} \inf\nolimits_{{\boldsymbol{b}} \in K}\|{\boldsymbol{y}}-{\boldsymbol{b}}\| \\&= d(A_n{\boldsymbol{x}},K_m)+\sup\nolimits_{{\boldsymbol{y}}\in K_m}d({\boldsymbol{y}},K).\end{split}\end{equation*}
Since
![]() $d({\boldsymbol{\eta}},K)=\lim_n d(A_n{\boldsymbol{x}}, K)$
by the continuity of
$d({\boldsymbol{\eta}},K)=\lim_n d(A_n{\boldsymbol{x}}, K)$
by the continuity of
![]() $d(\cdot,K)$
, it is sufficient to show that both
$d(\cdot,K)$
, it is sufficient to show that both
![]() $d(A_n{\boldsymbol{x}}, K_m)$
and
$d(A_n{\boldsymbol{x}}, K_m)$
and
![]() $\sup_{{\boldsymbol{y}} \in K_m} d({\boldsymbol{y}},K)$
are sufficiently small if n is sufficiently large and m is chosen properly.
$\sup_{{\boldsymbol{y}} \in K_m} d({\boldsymbol{y}},K)$
are sufficiently small if n is sufficiently large and m is chosen properly.
To this aim, fix
![]() $\varepsilon >0$
and choose
$\varepsilon >0$
and choose
![]() $m \in \textbf{N}$
such that
$m \in \textbf{N}$
such that
![]() $\sup\nolimits_{{\boldsymbol{y}}\in K_m}d({\boldsymbol{y}},K)\le\; {\varepsilon}/{2}$
. Indeed, it is sufficient to choose
$\sup\nolimits_{{\boldsymbol{y}}\in K_m}d({\boldsymbol{y}},K)\le\; {\varepsilon}/{2}$
. Indeed, it is sufficient to choose
![]() $m \in \textbf{N}$
such that
$m \in \textbf{N}$
such that
![]() $d({\boldsymbol{x}}_n, \textrm{L}_{{\boldsymbol{x}}})< \; {\varepsilon}/{2}$
for all
$d({\boldsymbol{x}}_n, \textrm{L}_{{\boldsymbol{x}}})< \; {\varepsilon}/{2}$
for all
![]() $n\ge m$
: indeed, in the opposite, the subsequence
$n\ge m$
: indeed, in the opposite, the subsequence
![]() $({\boldsymbol{x}}_j)_{j \in J}$
, where
$({\boldsymbol{x}}_j)_{j \in J}$
, where
![]() $J \;:\!=\; \{n\in \textbf{N}\;:\; d({\boldsymbol{x}}_n, \textrm{L}_{{\boldsymbol{x}}})\ge \; {\varepsilon}/{2}\}$
, would be bounded and without any accumulation point, which is impossible. Now pick
$J \;:\!=\; \{n\in \textbf{N}\;:\; d({\boldsymbol{x}}_n, \textrm{L}_{{\boldsymbol{x}}})\ge \; {\varepsilon}/{2}\}$
, would be bounded and without any accumulation point, which is impossible. Now pick
![]() ${\boldsymbol{y}} \in K_m$
so that
${\boldsymbol{y}} \in K_m$
so that
![]() ${\boldsymbol{y}}=\sum_j \lambda_{i_j} {\boldsymbol{x}}_{i_j}$
for some strictly increasing sequence
${\boldsymbol{y}}=\sum_j \lambda_{i_j} {\boldsymbol{x}}_{i_j}$
for some strictly increasing sequence
![]() $(i_j)$
of positive integers such that
$(i_j)$
of positive integers such that
![]() $i_1 \ge m$
and some real nonnegative sequence
$i_1 \ge m$
and some real nonnegative sequence
![]() $(\lambda_{i_j})$
with
$(\lambda_{i_j})$
with
![]() $\sum_{j} \lambda_{i_j}=1$
. It follows that
$\sum_{j} \lambda_{i_j}=1$
. It follows that
Suppose for the moment that A has nonnegative entries. Since A is regular, we get
![]() $\lim_n \sum_i a_{n,i}=1$
and
$\lim_n \sum_i a_{n,i}=1$
and
![]() $\lim_n \sum_{i<m}a_{n,i}=0$
by the Silverman–Toeplitz characterisation, hence
$\lim_n \sum_{i<m}a_{n,i}=0$
by the Silverman–Toeplitz characterisation, hence
![]() $\lim_n\sum_{i\ge m} a_{n,i}=1$
and there exists
$\lim_n\sum_{i\ge m} a_{n,i}=1$
and there exists
![]() $n_0 \in \textbf{N}$
such that
$n_0 \in \textbf{N}$
such that
![]() $\sum_{i\ge m} a_{n,i} \ge \; {1}/{2}$
for all
$\sum_{i\ge m} a_{n,i} \ge \; {1}/{2}$
for all
![]() $n\ge n_0$
. Thus, for each
$n\ge n_0$
. Thus, for each
![]() $n\ge n_0$
, we obtain that
$n\ge n_0$
, we obtain that
![]() $ d(A_n{\boldsymbol{x}},K_m)=\|A_n{\boldsymbol{x}}-Q_m(A_n{\boldsymbol{x}})\| \le \alpha_n+\beta_n+\gamma_n,$
where
$ d(A_n{\boldsymbol{x}},K_m)=\|A_n{\boldsymbol{x}}-Q_m(A_n{\boldsymbol{x}})\| \le \alpha_n+\beta_n+\gamma_n,$
where
and
Recalling that
![]() $\kappa=\sup_n \|{\boldsymbol{x}}_n\|$
, it is easy to see that
$\kappa=\sup_n \|{\boldsymbol{x}}_n\|$
, it is easy to see that
In addition, setting
![]() $t_n \;:\!=\; \sum_{i\ge m}a_{n,i}/\sum_i a_{n,i} \in [0,1]$
for all
$t_n \;:\!=\; \sum_{i\ge m}a_{n,i}/\sum_i a_{n,i} \in [0,1]$
for all
![]() $n\ge n_0$
, we get
$n\ge n_0$
, we get
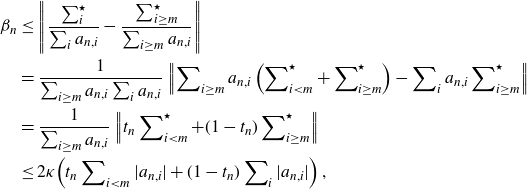 \begin{equation}\begin{split}\beta_n&\le \left\| \frac{\sum_i^\star}{\sum_i a_{n,i}}-\frac{\sum_{i\ge m}^\star}{\sum_{i\ge m} a_{n,i}}\right\|\\&=\frac{1}{\sum\nolimits_{i\ge m}a_{n,i}\sum\nolimits_{i}a_{n,i}}\left\| \sum\nolimits_{i\ge m}a_{n,i}\left(\sum\nolimits_{i< m}^\star+\sum\nolimits_{i\ge m}^\star \right)-\sum\nolimits_ia_{n,i}\sum\nolimits_{i\ge m}^\star\right\|\\&=\frac{1}{\sum\nolimits_{i\ge m}a_{n,i}}\left\| t_n\sum\nolimits_{i< m}^\star +(1-t_n)\sum\nolimits_{i\ge m}^\star\right\|\\&\le 2\kappa\!\left( t_n \sum\nolimits_{i<m} |a_{n,i}|+(1-t_n)\sum\nolimits_{i} |a_{n,i}|\right),\end{split}\end{equation}
\begin{equation}\begin{split}\beta_n&\le \left\| \frac{\sum_i^\star}{\sum_i a_{n,i}}-\frac{\sum_{i\ge m}^\star}{\sum_{i\ge m} a_{n,i}}\right\|\\&=\frac{1}{\sum\nolimits_{i\ge m}a_{n,i}\sum\nolimits_{i}a_{n,i}}\left\| \sum\nolimits_{i\ge m}a_{n,i}\left(\sum\nolimits_{i< m}^\star+\sum\nolimits_{i\ge m}^\star \right)-\sum\nolimits_ia_{n,i}\sum\nolimits_{i\ge m}^\star\right\|\\&=\frac{1}{\sum\nolimits_{i\ge m}a_{n,i}}\left\| t_n\sum\nolimits_{i< m}^\star +(1-t_n)\sum\nolimits_{i\ge m}^\star\right\|\\&\le 2\kappa\!\left( t_n \sum\nolimits_{i<m} |a_{n,i}|+(1-t_n)\sum\nolimits_{i} |a_{n,i}|\right),\end{split}\end{equation}
where
![]() $\sum_{i \in I}^\star$
stands for
$\sum_{i \in I}^\star$
stands for
![]() $\sum_{i \in I}a_{n,i}{\boldsymbol{x}}_i$
. Note that the hypothesis that the entries of A are nonnegative has been used only in the first line of (6), so that
$\sum_{i \in I}a_{n,i}{\boldsymbol{x}}_i$
. Note that the hypothesis that the entries of A are nonnegative has been used only in the first line of (6), so that
![]() $\sum^\star_{i\ge m}/\sum_{i\ge m}a_{n,i} \in K_m$
. Since
$\sum^\star_{i\ge m}/\sum_{i\ge m}a_{n,i} \in K_m$
. Since
![]() $\lim_n \sum_{i<m}|a_{n,i}|=0$
,
$\lim_n \sum_{i<m}|a_{n,i}|=0$
,
![]() $\lim_n t_n=1$
, and
$\lim_n t_n=1$
, and
![]() $\sup_n \sum_i |a_{n,i}|<\infty$
by the regularity of A, it follows that all
$\sup_n \sum_i |a_{n,i}|<\infty$
by the regularity of A, it follows that all
![]() $\alpha_n, \beta_n, \gamma_n$
are smaller than
$\alpha_n, \beta_n, \gamma_n$
are smaller than
![]() ${\varepsilon}/{6}$
if n is sufficiently large. Therefore
${\varepsilon}/{6}$
if n is sufficiently large. Therefore
![]() $d(A_n{\boldsymbol{x}},K)\le \varepsilon$
and, since
$d(A_n{\boldsymbol{x}},K)\le \varepsilon$
and, since
![]() $\varepsilon$
is arbitrary, we conclude that
$\varepsilon$
is arbitrary, we conclude that
![]() ${\boldsymbol{\eta}}=\lim_n A_n{\boldsymbol{x}} \in K$
.
${\boldsymbol{\eta}}=\lim_n A_n{\boldsymbol{x}} \in K$
.
Lastly, suppose that A is a regular matrix such that
![]() $\lim_n \sum_i |a_{n,i}|=1$
and let
$\lim_n \sum_i |a_{n,i}|=1$
and let
![]() $B=(b_{n,i})$
be the nonnegative regular matrix defined by
$B=(b_{n,i})$
be the nonnegative regular matrix defined by
![]() $b_{n,i}=|a_{n,i}|$
for all
$b_{n,i}=|a_{n,i}|$
for all
![]() $n,i \in \textbf{N}$
. Considering that
$n,i \in \textbf{N}$
. Considering that
and that
![]() $\lim_n\sum\nolimits_i |a_{n,i}-|a_{n,i}||= 0$
because
$\lim_n\sum\nolimits_i |a_{n,i}-|a_{n,i}||= 0$
because
![]() $\lim_n \sum_i a_{n,i}=\lim_n\sum_i |a_{n,i}|=1$
, we conclude that
$\lim_n \sum_i a_{n,i}=\lim_n\sum_i |a_{n,i}|=1$
, we conclude that
![]() $d(A_n{\boldsymbol{x}}, K_m) \le 2\varepsilon$
whenever n is sufficiently large. The claim follows as before.
$d(A_n{\boldsymbol{x}}, K_m) \le 2\varepsilon$
whenever n is sufficiently large. The claim follows as before.
The following corollary is immediate:
Corollary 4·4. Let
![]() ${\boldsymbol{x}}=({\boldsymbol{x}}_n)$
be a bounded sequence taking values in
${\boldsymbol{x}}=({\boldsymbol{x}}_n)$
be a bounded sequence taking values in
![]() $\mathbf{R}^k$
, and fix a nonnegative regular matrix A. Then inclusion (5) holds.
$\mathbf{R}^k$
, and fix a nonnegative regular matrix A. Then inclusion (5) holds.
Remark 4·5. Inclusion (5) fails for an arbitrary regular matrix: indeed, let
![]() $A=(a_{n,i})$
be the matrix defined by
$A=(a_{n,i})$
be the matrix defined by
![]() $a_{n,2n}=2$
,
$a_{n,2n}=2$
,
![]() $a_{n,2n-1}=-1$
for all
$a_{n,2n-1}=-1$
for all
![]() $n \in \textbf{N}$
, and
$n \in \textbf{N}$
, and
![]() $a_{n,i}=0$
otherwise. Set also
$a_{n,i}=0$
otherwise. Set also
![]() $k=1$
and let x be the sequence such that
$k=1$
and let x be the sequence such that
![]() $x_n=(\!-\!1)^n$
for all
$x_n=(\!-\!1)^n$
for all
![]() $n\in \textbf{N}$
. Then A is regular and
$n\in \textbf{N}$
. Then A is regular and
![]() $\lim Ax=3 \notin \{-1,1\}=\textrm{K}\text{-}\textrm{core}(x)$
.
$\lim Ax=3 \notin \{-1,1\}=\textrm{K}\text{-}\textrm{core}(x)$
.
Remark 4·6. Proposition 4·3 keeps holding on a (possibly infinite dimensional) Hilbert space X with the following provisoes: replace the definition of
![]() $\textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})$
with the closure of
$\textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})$
with the closure of
![]() $\textrm{co}\,\textrm{L}_{{\boldsymbol{x}}}$
(this coincides in the case that
$\textrm{co}\,\textrm{L}_{{\boldsymbol{x}}}$
(this coincides in the case that
![]() $X=\textbf{R}^k$
) and assume that the sequence
$X=\textbf{R}^k$
) and assume that the sequence
![]() ${\boldsymbol{x}}$
is contained in a compact set (so that
${\boldsymbol{x}}$
is contained in a compact set (so that
![]() $\textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})$
is also nonempty).
$\textrm{K}\text{-}\textrm{core}({\boldsymbol{x}})$
is also nonempty).
With these premises, we can strenghten Theorem 4·2 as follows.
Theorem 4·7. The set
![]() $\{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I},A)=\Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager, provided that
$\{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I},A)=\Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager, provided that
![]() $\mathcal{I}$
is a meager ideal and A is a regular matrix such that
$\mathcal{I}$
is a meager ideal and A is a regular matrix such that
![]() $\lim_n\sum_i |a_{n,i}|=1$
.
$\lim_n\sum_i |a_{n,i}|=1$
.
Proof. Let us suppose that
![]() $A=(a_{n,i})$
is nonnegative regular matrix, i.e.,
$A=(a_{n,i})$
is nonnegative regular matrix, i.e.,
![]() $a_{n,i}\ge 0$
for all
$a_{n,i}\ge 0$
for all
![]() $n,i \in \textbf{N}$
, and fix a meager ideal
$n,i \in \textbf{N}$
, and fix a meager ideal
![]() $\mathcal{I}$
, a real
$\mathcal{I}$
, a real
![]() $x \in (0,1]$
, and integers
$x \in (0,1]$
, and integers
![]() $b\ge 2$
,
$b\ge 2$
,
![]() $k\ge 1$
. Thanks to Theorem 4·2, it is sufficient to show that every accumulation point of the sequence
$k\ge 1$
. Thanks to Theorem 4·2, it is sufficient to show that every accumulation point of the sequence
![]() $(A_n{\boldsymbol{\pi}}_{b}^k(x)\;:\; n\ge 1)$
is contained in the convex hull of the set of accumulation points of
$(A_n{\boldsymbol{\pi}}_{b}^k(x)\;:\; n\ge 1)$
is contained in the convex hull of the set of accumulation points of
![]() $({\boldsymbol{\pi}}_{b,n}^k(x)\;:\; n\ge 1)$
, which is in turn contained into
$({\boldsymbol{\pi}}_{b,n}^k(x)\;:\; n\ge 1)$
, which is in turn contained into
![]() $\Delta_b^k$
. This follows by Proposition 4·3.
$\Delta_b^k$
. This follows by Proposition 4·3.
Since the family of meager sets is a
![]() $\sigma$
-ideal, the following is immediate by Theorem 4·7.
$\sigma$
-ideal, the following is immediate by Theorem 4·7.
Corollary 4·8. Let
![]() $\mathscr{A}$
be a countable family of regular matrices such that
$\mathscr{A}$
be a countable family of regular matrices such that
![]() $\lim_n\sum_i |a_{n,i}|=1$
. Then the set
$\lim_n\sum_i |a_{n,i}|=1$
. Then the set
![]() $\{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I},A)=\Delta_{b}^k \text{ for all }b\ge 2, k\ge 1, \text{ and all }A \in \mathscr{A}\,\}$
is comeager, provided that
$\{x \in (0,1]\;:\; \Gamma_b^k (x,\mathcal{I},A)=\Delta_{b}^k \text{ for all }b\ge 2, k\ge 1, \text{ and all }A \in \mathscr{A}\,\}$
is comeager, provided that
![]() $\mathcal{I}$
is a meager ideal.
$\mathcal{I}$
is a meager ideal.
It is worth to remark that the main result [
Reference Hyde, Laschos, Olsen, Petrykiewicz and Shaw15
] is obtained as an instance of Corollary 4·8, letting
![]() $\mathscr{A}$
be the set of iterates of the Cesàro matrix (note that they are nonnegative regular matrices), and setting
$\mathscr{A}$
be the set of iterates of the Cesàro matrix (note that they are nonnegative regular matrices), and setting
![]() $k=1$
and
$k=1$
and
![]() $\mathcal{I}=\textrm{Fin}$
. The same holds for the iterates of the Hölder matrix and the logarithmic Riesz matrix as in [
Reference Olsen and West24
, sections 3 and 4].
$\mathcal{I}=\textrm{Fin}$
. The same holds for the iterates of the Hölder matrix and the logarithmic Riesz matrix as in [
Reference Olsen and West24
, sections 3 and 4].
Next, we show that the hypothesis
![]() $\lim_n \sum_i |a_{n,i}|=1$
for the entries of the regular matrix in Theorem 4·7 cannot be removed.
$\lim_n \sum_i |a_{n,i}|=1$
for the entries of the regular matrix in Theorem 4·7 cannot be removed.
Example 4·9. Let
![]() $A=(a_{n,i})$
be the matrix such that
$A=(a_{n,i})$
be the matrix such that
![]() $a_{n,(2n-1)!}=-1$
and
$a_{n,(2n-1)!}=-1$
and
![]() $a_{n,(2n)!}=2$
for all
$a_{n,(2n)!}=2$
for all
![]() $n \in \textbf{N}$
, and
$n \in \textbf{N}$
, and
![]() $a_{n,i}=0$
otherwise. It is easily seen that A is regular. Then, set
$a_{n,i}=0$
otherwise. It is easily seen that A is regular. Then, set
![]() $b=2$
,
$b=2$
,
![]() $k=1$
, and
$k=1$
, and
![]() $\mathcal{I}=\textrm{Fin}$
. We claim that the set of all
$\mathcal{I}=\textrm{Fin}$
. We claim that the set of all
![]() $x \in (0,1]$
such that 2 is an accumulation point of the sequence
$x \in (0,1]$
such that 2 is an accumulation point of the sequence
![]() $\pi_{2,1}(x)=(\pi_{2,1,n}(x)\;:\; n\ge 1)$
is comeager. Indeed, its complement can be rewritten as
$\pi_{2,1}(x)=(\pi_{2,1,n}(x)\;:\; n\ge 1)$
is comeager. Indeed, its complement can be rewritten as
![]() $\bigcup_{m,p}S_{m,p}$
, where
$\bigcup_{m,p}S_{m,p}$
, where
Let
![]() $x^\star\in (0,1]$
such that
$x^\star\in (0,1]$
such that
![]() $d_{2,n}(x^\star)=1$
if and only if
$d_{2,n}(x^\star)=1$
if and only if
![]() $(2i-1)!\le n<(2i)!$
for some
$(2i-1)!\le n<(2i)!$
for some
![]() $i \in \textbf{N}$
. Then it is easily seen that
$i \in \textbf{N}$
. Then it is easily seen that
![]() $\lim_n \pi_{2,1,n}(x^\star)=2$
. Along the same lines of the proof of Theorem 4·2, it follows that each
$\lim_n \pi_{2,1,n}(x^\star)=2$
. Along the same lines of the proof of Theorem 4·2, it follows that each
![]() $S_{m,p}$
is meager. We conclude that
$S_{m,p}$
is meager. We conclude that
![]() $\{x \in (0,1]\;:\; \Gamma_2^1 (x,\textrm{Fin},A)=\Delta_{2}^1\}$
is meager, which proves that the condition
$\{x \in (0,1]\;:\; \Gamma_2^1 (x,\textrm{Fin},A)=\Delta_{2}^1\}$
is meager, which proves that the condition
![]() $\lim_n \sum_i |a_{n,i}|=1$
in the statement of Theorem 4·7 cannot be removed.
$\lim_n \sum_i |a_{n,i}|=1$
in the statement of Theorem 4·7 cannot be removed.
In addition, the main result in [
Reference Stylianou27
] states that Theorem 4·2, specialised to the case
![]() $\mathcal{I}=\textrm{Fin}$
and
$\mathcal{I}=\textrm{Fin}$
and
![]() $k=1$
, can be further strengtened so that the set
$k=1$
, can be further strengtened so that the set
![]() $$\{ x \in (0,1]\;:\;\Gamma _b^1(x,{\rm{Fin}},A) \supseteq \Delta _b^1$$
for all
$$\{ x \in (0,1]\;:\;\Gamma _b^1(x,{\rm{Fin}},A) \supseteq \Delta _b^1$$
for all
![]() $$b \ge 2$$
and all regular A} is comeager. Taking into account the argument in the proof of Theorem 4·7, this would imply that the set
$$b \ge 2$$
and all regular A} is comeager. Taking into account the argument in the proof of Theorem 4·7, this would imply that the set
should be comeager. However, this is false as it is shown in the next example.
Example 4·10. For each
![]() $y \in (0,1]$
, let
$y \in (0,1]$
, let
![]() $(e_{y,k}\;:\; k\ge 1)$
be the increasing enumeration of the infinite set
$(e_{y,k}\;:\; k\ge 1)$
be the increasing enumeration of the infinite set
![]() $\{n \in \textbf{N}\;:\; d_{2,n}(y)=1\}$
. Then, let
$\{n \in \textbf{N}\;:\; d_{2,n}(y)=1\}$
. Then, let
![]() $\mathscr{A}=\{A_y\;:\; y \in (0,1]\}$
be family of matrices
$\mathscr{A}=\{A_y\;:\; y \in (0,1]\}$
be family of matrices
![]() $A_y=\left(a^{(y)}_{n,i}\right)$
with entries in
$A_y=\left(a^{(y)}_{n,i}\right)$
with entries in
![]() $\{0,1\}$
so that
$\{0,1\}$
so that
![]() $a^{(y)}_{n,i}=1$
if and only if
$a^{(y)}_{n,i}=1$
if and only if
![]() $e_{y,n}=i$
for all
$e_{y,n}=i$
for all
![]() $y \in (0,1]$
and all
$y \in (0,1]$
and all
![]() $n,i \in \textbf{N}$
. Then each
$n,i \in \textbf{N}$
. Then each
![]() $A_y$
is a nonnegative regular matrix. It follows, for each ideal
$A_y$
is a nonnegative regular matrix. It follows, for each ideal
![]() $\mathcal{I}$
,
$\mathcal{I}$
,
Indeed, for each
![]() $x \in (0,1]$
, the sequence
$x \in (0,1]$
, the sequence
![]() ${\boldsymbol{\pi}}_2^1(x)=({\boldsymbol{\pi}}_{2,n}^1(x)\;:\;n\ge 1)$
has an accumulation point
${\boldsymbol{\pi}}_2^1(x)=({\boldsymbol{\pi}}_{2,n}^1(x)\;:\;n\ge 1)$
has an accumulation point
![]() ${\boldsymbol{\eta}} \in \Delta_2^1$
. Hence there exists a subsequence
${\boldsymbol{\eta}} \in \Delta_2^1$
. Hence there exists a subsequence
![]() $({\boldsymbol{\pi}}_{2,n_k}^1(x)\;:\;k\ge 1)$
which is convergent to
$({\boldsymbol{\pi}}_{2,n_k}^1(x)\;:\;k\ge 1)$
which is convergent to
![]() ${\boldsymbol{\eta}}$
. Equivalently,
${\boldsymbol{\eta}}$
. Equivalently,
![]() $\lim A_y{\boldsymbol{\pi}}_2^1(x)={\boldsymbol{\eta}}$
, where
$\lim A_y{\boldsymbol{\pi}}_2^1(x)={\boldsymbol{\eta}}$
, where
![]() $y\in (0,1]$
is defined such that
$y\in (0,1]$
is defined such that
![]() $e_{y,k}=n_k$
for all
$e_{y,k}=n_k$
for all
![]() $k \in \textbf{N}$
. Therefore
$k \in \textbf{N}$
. Therefore
![]() $\{{\boldsymbol{\eta}}\}=\Gamma_2^1 (x,\mathcal{I},A_y)\neq \Delta_{2}^1$
. in particular, the set defined in (7) is empty.
$\{{\boldsymbol{\eta}}\}=\Gamma_2^1 (x,\mathcal{I},A_y)\neq \Delta_{2}^1$
. in particular, the set defined in (7) is empty.
Lastly, the analogues of Theorem 4·2 and Theorem 4·7 hold for
![]() $\mathcal{I}$
-limit points, if
$\mathcal{I}$
-limit points, if
![]() $\mathcal{I}$
is an
$\mathcal{I}$
is an
![]() $F_\sigma$
-ideal or an analytic P-ideal. Indeed, denoting with
$F_\sigma$
-ideal or an analytic P-ideal. Indeed, denoting with
![]() $\Lambda_b^k(x,\mathcal{I},A)$
the set of
$\Lambda_b^k(x,\mathcal{I},A)$
the set of
![]() $\mathcal{I}$
-limit points of the sequence
$\mathcal{I}$
-limit points of the sequence
![]() $(A_n{\boldsymbol{\pi}}_b^k(x)\;:\; n\ge 1)$
, we obtain:
$(A_n{\boldsymbol{\pi}}_b^k(x)\;:\; n\ge 1)$
, we obtain:
Theorem 4·11. Let A be a regular matrix and let
![]() $\mathcal{I}$
be an
$\mathcal{I}$
be an
![]() $F_\sigma$
-ideal or an analytic P-ideal. Then the set
$F_\sigma$
-ideal or an analytic P-ideal. Then the set
![]() $\{x \in (0,1]\;:\; \Lambda_b^k (x,\mathcal{I},A)\supseteq \Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager.
$\{x \in (0,1]\;:\; \Lambda_b^k (x,\mathcal{I},A)\supseteq \Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager.
Moreover, the set
![]() $\{x \in (0,1]\;:\; \Lambda_b^k (x,\mathcal{I},A)=\Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager if, in addition, A satisfies
$\{x \in (0,1]\;:\; \Lambda_b^k (x,\mathcal{I},A)=\Delta_{b}^k \text{ for all }b\ge 2, k\ge 1\}$
is comeager if, in addition, A satisfies
![]() $\lim_n\sum_i |a_{n,i}|=1$
.
$\lim_n\sum_i |a_{n,i}|=1$
.
Proof. The first part goes along the same lines of the proof of Theorem 2·3. Here, we replace
![]() ${\boldsymbol{\pi}}_b^k(x)$
with
${\boldsymbol{\pi}}_b^k(x)$
with
![]() $(A_n{\boldsymbol{\pi}}_b^k(x)\;:\; n\ge 1)$
and using the chain of inequalities (4): more precisely, we consider
$(A_n{\boldsymbol{\pi}}_b^k(x)\;:\; n\ge 1)$
and using the chain of inequalities (4): more precisely, we consider
![]() $j^{\prime\prime}\in \textbf{N}$
such that
$j^{\prime\prime}\in \textbf{N}$
such that
![]() $\varphi(\{n \in [j^\prime, j^{\prime\prime}]\;:\; \|A_n {\boldsymbol{\pi}}^k_b(x^\prime)-{\boldsymbol{\eta}}\|\le \; {1}/{2t}\})\ge \; {1}/{2},$
and, taking into considering (4), we define
$\varphi(\{n \in [j^\prime, j^{\prime\prime}]\;:\; \|A_n {\boldsymbol{\pi}}^k_b(x^\prime)-{\boldsymbol{\eta}}\|\le \; {1}/{2t}\})\ge \; {1}/{2},$
and, taking into considering (4), we define
![]() $V \;:\!=\; \{x \in (0,1]\;:\; d_{b,i}(x)=d_{b,i}(x^\star) \text{ for all }i=1,\ldots,k+j^{\prime\prime\prime}\}$
, where
$V \;:\!=\; \{x \in (0,1]\;:\; d_{b,i}(x)=d_{b,i}(x^\star) \text{ for all }i=1,\ldots,k+j^{\prime\prime\prime}\}$
, where
![]() $j^{\prime\prime\prime}$
is a sufficiently large integer such that
$j^{\prime\prime\prime}$
is a sufficiently large integer such that
![]() $\sum_{i>j^{\prime\prime\prime}}|a_{n,i}|\le \; {1}/{2t}$
for all
$\sum_{i>j^{\prime\prime\prime}}|a_{n,i}|\le \; {1}/{2t}$
for all
![]() $n \in [j^\prime, j^{\prime\prime}]$
.
$n \in [j^\prime, j^{\prime\prime}]$
.
The second part follows, as in Theorem 4·7, by the fact that every accumulation point of
![]() $(A_n{\boldsymbol{\pi}}_b^k(x)\;:\; n\ge 1)$
belongs to
$(A_n{\boldsymbol{\pi}}_b^k(x)\;:\; n\ge 1)$
belongs to
![]() $\Delta_b^k$
.
$\Delta_b^k$
.
Acknowledgments
P. Leonetti is grateful to PRIN 2017 (grant 2017CY2NCA) for financial support.