Hostname: page-component-5cf477f64f-mgq6s Total loading time: 0 Render date: 2025-04-07T09:41:21.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Moments of the Hurwitz zeta function on the critical line

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  28 November 2022

ANURAG SAHAY
ANURAG SAHAY*
Affiliation:
Department of Mathematics, University of Rochester, Hylan Building, 140 Trustee Road, Rochester, NY 14620, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the moments 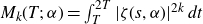$M_k(T;\,\alpha) = \int_T^{2T} |\zeta(s,\alpha)|^{2k}\,dt$ of the Hurwitz zeta function 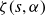$\zeta(s,\alpha)$ on the critical line, 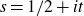$s = 1/2 + it$ with a rational shift 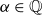$\alpha \in \mathbb{Q}$ . We conjecture, in analogy with the Riemann zeta function, that 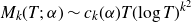$M_k(T;\,\alpha) \sim c_k(\alpha) T (\!\log T)^{k^2}$ . Using heuristics from analytic number theory and random matrix theory, we conjecturally compute 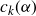$c_k(\alpha)$ . In the process, we investigate moments of products of Dirichlet L-functions on the critical line. We prove some of our conjectures for the cases 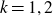$k = 1,2$ .

MSC classification

Primary: 11M35: Hurwitz and Lerch zeta functions
Secondary: 11M06: $zeta (s)$ and $L(s, chi)$
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 3 , May 2023 , pp. 631 - 661
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, J.. Summation formulae and zeta functions. PhD. thesis. Stockholm University (2006).Google Scholar
Andrade, J. and Shamesaldeen, A.. Hybrid Euler–Hadamard product for dirichlet L-functions with prime conductors over function fields. Preprint, arXiv:1909.08953v1 (2019).Google Scholar
Andrade, J. C., Gonek, S. M. and Keating, J. P.. Truncated product representations for L-functions in the hyperelliptic ensemble. Mathematika. 64(1) (2018), 137–158.Google Scholar
Bettin, S., Bui, H. M., Li, X. and Radziwiłł, M.. A quadratic divisor problem and moments of the Riemann zeta-function. J. Eur. Math. Soc. (JEMS), 22(12) (2020), 3953–3980.Google Scholar
Bettin, S., Chandee, V. and Radziwiłł, M.. The mean square of the product of the Riemann zeta-function with Dirichlet polynomials. J. Reine Angew. Math., 729 (2017), 51–79.CrossRefGoogle Scholar
Bourgain, J., Garaev, M. Z., Konyagin, S. V. and Shparlinski, I. E.. Multiplicative congruences with variables from short intervals. J. Anal. Math. 124 (2014), 117–147.CrossRefGoogle Scholar
Bui, H. M. and Florea, A.. Hybrid Euler–Hadamard product for quadratic Dirichlet L-functions in function fields. Proc. Lond. Math. Soc. (3), 117(1) (2018), 65–99.Google Scholar
Bui, H. M., Gonek, S. M. and Milinovich, M. B.. A hybrid Euler–Hadamard product and moments of $\zeta^{\prime}(\rho)$ . Forum Math. 27(3) (2015), 1799–1828.CrossRefGoogle Scholar
Bui, H. M. and Keating, J. P.. On the mean values of Dirichlet L-functions. Proc. London Math. Soc. (3), 95(2) (2007), 273–298.Google Scholar
Bui, H. M. and Keating, J. P.. On the mean values of L-functions in orthogonal and symplectic families. Proc. London Math. Soc. (3), 96(2) (2008), 335–366.Google Scholar
Cassels, J. W. S.. Footnote to a note of Davenport and Heilbronn. J. London Math. Soc. 36 (1961), 177–184.CrossRefGoogle Scholar
Conrey, J. B., Farmer, D. W., Keating, J. P., Rubinstein, M. O. and Snaith, N. C.. Integral moments of L-functions. Proc. London Math. Soc. (3), 91(1) (2005), 33–104.Google Scholar
Conrey, J. B. and Ghosh, A.. On mean values of the zeta-function. Mathematika 31(1) (1984), 159–161.CrossRefGoogle Scholar
Conrey, J. B. and Gonek, S. M.. High moments of the Riemann zeta-function. Duke Math. J. 107(3) (2001), 577–604.Google Scholar
Davenport, H. and Heilbronn, H.. On the zeros of certain Dirichlet series. J. London Math. Soc. 11(3) (1936), 181–185.Google Scholar
Djanković, G.. Euler–Hadamard products and power moments of symmetric square L-functions. Int. J. Number Theory 9(3) (2013), 621–639.Google Scholar
Gonek, S., Hughes, C. and Keating, J.. A hybrid Euler–Hadamard product for the Riemann zeta function. Duke Math. J. 136(3) (2007), 507–549.Google Scholar
Gonek, S. M.. Analytic properties of zeta and L-functions. PhD. thesis. University of Michigan (1979).Google Scholar
Gonek, S. M.. The zeros of Hurwitz’s zeta function on $\sigma ={1/2}$ . In Analytic Number Theory (Philadelphia, Pa., 1980), Lecture Notes in Math. vol. 899 (Springer, Berlin-New York, 1981), pp. 129–140.Google Scholar
Hardy, G. H. and Littlewood, J. E.. Contributions to the theory of the riemann zeta-function and the theory of the distribution of primes. Acta Math. 41(1) (1916), 119–196.Google Scholar
Harper, A.. Sharp conditional bounds for moments of the Riemann zeta function. Preprint arXiv:1305.4618, (2013).Google Scholar
Heap, W.. The twisted second moment of the Dedekind zeta function of a quadratic field. Int. J. Number Theory 10(1) (2014), 235–281.Google Scholar
Heap, W.. Moments of the Dedekind zeta function and other non-primitive L-functions. Math. Proc. Camb. Phil. Soc. 170(1) (2021), 191–219.Google Scholar
Heap, W.. On the splitting conjecture in the hybrid model for the Riemann zeta function. Preprint, arXiv:2102.02092, (2021).Google Scholar
Heap, W., Radziwiłł, M. and Soundararajan, K.. Sharp upper bounds for fractional moments of the Riemann zeta function. Q. J. Math. 70(4) (2019), 1387–1396.Google Scholar
Heap, W., Sahay, A. and Wooley, T. D.. A paucity problem associated with a shifted integer analogue of the divisor function. J. Number Theory, in preparation (2022).Google Scholar
Heap, W. and Soundararajan, K.. Lower bounds for moments of zeta and L-functions revisited. Mathematika 68(1) (2022), 1–14.Google Scholar
Heath–Brown, D. R.. Fractional moments of the Riemann zeta function. J. London Math. Soc. (2), 24(1) (1981), 65–78.Google Scholar
Hughes, C. P. and Young, M. P.. The twisted fourth moment of the Riemann zeta function. J. Reine Angew. Math. 641 (2010), 203–236.Google Scholar
Ingham, A. E.. Mean-value theorems in the theory of the Riemann zeta-function. Proc. London Math. Soc. (2), 27(4) (1927), 273–300.Google Scholar
Ishikawa, H.. A difference between the values of $|L(1/2+it,\chi_j)|$ and $|L(1/2+it,\chi_k)|$ . I. Comment. Math. Univ. St. Pauli 55(1) (2006), 41–66.Google Scholar
Keating, J. P. and Snaith, N. C.. Random matrix theory and $\zeta(1/2+it)$ . Comm. Math. Phys. 214(1) (2000), 57–89.CrossRefGoogle Scholar
Knopp, M. and Robins, S.. Easy proofs of Riemann’s functional equation for $\zeta(s)$ and of Lipschitz summation. Proc. Amer. Math. Soc. 129(7) (2001), 1915–1922.Google Scholar
Languasco, A. and Zaccagnini, A.. A note on Mertens’ formula for arithmetic progressions. J. Number Theory 127(1) (2007), 37–46.Google Scholar
Milinovich, M. B. and Turnage–Butterbaugh, C. L.. Moments of products of automorphic L-functions. J. Number Theory 139 (2014), 175–204.Google Scholar
Radziwiłł, M. and Soundararajan, K.. Continuous lower bounds for moments of zeta and L-functions. Mathematika 59(1) (2013), 119–128.Google Scholar
Ramachandra, K.. Some remarks on the mean value of the Riemann zeta function and other Dirichlet series. I. Hardy–Ramanujan J. 1:15, 1978.Google Scholar
Ramachandra, K.. Some remarks on the mean value of the Riemann zeta function and other Dirichlet series. II. Hardy–Ramanujan J. 3 (1980), 1–24.Google Scholar
Ramachandra, K.. Some remarks on the mean value of the Riemann zeta function and other Dirichlet series. III. Ann. Acad. Sci. Fenn. Ser. A I Math. 5 (1980), 145–158.Google Scholar
Rane, V. V.. On the mean square value of Dirichlet L-series. J. London Math. Soc. (2), 21(2) (1980), 203–215.Google Scholar
Soundararajan, K.. Moments of the Riemann zeta function. Ann. of Math. (2), 170(2) (2009), 981–993.Google Scholar
Spira, R.. Zeros of Hurwitz zeta functions. Math. Comp. 30(136) (1976), 863–866.Google Scholar
Titchmarsh, E.. The theory of the Riemann zeta-function (The Clarendon Press, Oxford University Press, New York, second edition, 1986). Edited and with a preface by D. R. Heath–Brown.Google Scholar
Topacogullari, B.. The fourth moment of individual Dirichlet L-functions on the critical line. Math. Z. 298(1-2) (2021), 577–624.Google Scholar
Voronin, S. M.. The zeros of zeta-functions of quadratic forms. Trudy Mat. Inst. Steklov., 142(269) (1976), 135–147. Number theory, mathematical analysis and their applications.Google Scholar
Williams, K. S.. Mertens’ theorem for arithmetic progressions. J. Number Theory 6 (1974), 353–359.CrossRefGoogle Scholar
Wu, X.. The twisted mean square and critical zeros of Dirichlet L-functions. Math. Z. 293(1-2) (2019), 825–865.Google Scholar
Zhan, T.. On the mean square of Dirichlet L-functions. Acta Math. Sinica (N.S.), 8(2):204–224, 1992. A Chinese summary appears in Acta Math. Sinica 36 (1993), no. 3, 432.Google Scholar