Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T14:56:44.339Z Has data issue: false hasContentIssue false
  • English
  • Français

Metric properties of some fractal sets and applications of inverse pressure

Published online by Cambridge University Press:  20 November 2009

EUGEN MIHAILESCU
EUGEN MIHAILESCU*
Affiliation:
Institute of Mathematics “Simion Stoilow” of the Romanian Academy, P.O. Box 1-764, RO 014700, Bucharest, Romania. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider iterations of smooth non-invertible maps on manifolds of real dimension 4, which are hyperbolic, conformal on stable manifolds and finite-to-one on basic sets. The dynamics of non-invertible maps can be very different than the one of diffeomorphisms, as was shown for example in [4, 7, 12, 17, 19], etc. In [13] we introduced a notion of inverse topological pressure P− which can be used for estimates of the stable dimension δs(x) (i.e the Hausdorff dimension of the intersection between the local stable manifold Wsr(x) and the basic set Λ, x ∈ Λ). In [10] it is shown that the usual Bowen equation is not always true in the case of non-invertible maps. By using the notion of inverse pressure P−, we showed in [13] that δs(x) ≤ ts(ϵ), where ts(ϵ) is the unique zero of the function t → P−(tφs, ϵ), for φs(y):= log|Dfs(y)|, y ∈ Λ and ϵ > 0 small. In this paper we prove that if Λ is not a repellor, then ts(ϵ) < 2 for any ϵ > 0 small enough. In [11] we showed that a holomorphic s-hyperbolic map on 2 has a global unstable set with empty interior. Here we show in a more general setting than in [11], that the Hausdorff dimension of the global unstable set Wu(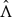) is strictly less than 4 under some technical derivative condition. In the non-invertible case we may have (infinitely) many unstable manifolds going through a point in Λ, and the number of preimages belonging to Λ may vary. In [17], Qian and Zhang studied the case of attractors for non-invertible maps and gave a condition for a basic set to be an attractor in terms of the pressure of the unstable potential. In our case the situation is different, since the local unstable manifolds may intersect both inside and outside Λ and they do not form a foliation like the stable manifolds. We prove here that the upper box dimension of Wsr(x) ∩ Λ is less than ts(ϵ) for any point x ∈ Λ. We give then an estimate of the Hausdorff dimension of Wu(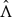) by a different technique, using the Holder continuity of the unstable manifolds with respect to their prehistories.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 148 , Issue 3 , May 2010 , pp. 553 - 572
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bedford, E. and Smillie, J.Polynomial diffeomorphisms of 2. Invent. Math. 103 (1991), 69–99.CrossRefGoogle Scholar
[2]Bowen, R. Equilibrium states and the ergodic theory of Anosov diffeomorphisms. Lecture Notes in Math. 470 (Springer 1973).Google Scholar
[3]Bowen, R.A horseshoe with positive measure. Invent. Math. 29, 203–204, 1975.CrossRefGoogle Scholar
[4]Bothe, H. G.Shift spaces and attractors in noninvertible horseshoes. Fund. Math. 152 (1997), no. 3, 267–289.Google Scholar
[5]Fornaess, J. E and Sibony, N.Hyperbolic maps on 2. Math. Ann. 311 (1998), 305–333.CrossRefGoogle Scholar
[6]Katok, A. and Hasselblatt, B.Introduction to the Modern Theory of Dynamical Systems Cambridge University Press (1995).CrossRefGoogle Scholar
[7]Liu, P. D. Invariant measures satisfying an equality relating entropy, folding entropy and negative Lyapunov exponents. Comm. Math. Physics (2008).CrossRefGoogle Scholar
[8]Manning, A. and McCluskey, H.Hausdorff dimension for horseshoes. Ergod. Th. and Dyn. Syst. 3 (1983), no. 2, 251–260.Google Scholar
[9]Mattila, P.Geometry of Sets and Measures in Euclidian Spaces (Cambridge University Press, 1995).CrossRefGoogle Scholar
[10]Mihailescu, E. Applications of thermodynamic formalism in complex dynamics on 2. Discrete and Cont. Dyn. Syst. vol. 7, no. 4 (2001), 821–836.Google Scholar
[11]Mihailescu, E.The set K − for hyperbolic non-invertible maps. Ergodic Th. and Dyn. Syst. 22 (2002), 873–887.Google Scholar
[12]Mihailescu, E. and Urbanski, M.Estimates for the stable dimension for holomorphic maps. Houston J. Math. 31, no. 2 (2005), 367–389.Google Scholar
[13]Mihailescu, E. and Urbanski, M.Inverse topological pressure with applications to holomorphic dynamics of several complex variables. Comm. Contemp. Math. 6, no. 4 (2004), 653–682.CrossRefGoogle Scholar
[14]Mihailescu, E. and Urbanski, M. Inverse pressure estimates and the independence of stable dimension. Canad. J. Math. vol. 60, no. 3 (2008), 658–684.Google Scholar
[15]Mihailescu, E. and Urbanski, M. Transversal families of hyperbolic skew products. Discrete and Cont. Dyn. Syst. vol. 21, no. 3 (2008), 907–929.Google Scholar
[16]Nitecki, Z. and Przytycki, F.Preimage entropy for maps. Inter. J. Bifur. Class Appl. Sci. Engr. 9, (1999), no. 9, 1815–1843.CrossRefGoogle Scholar
[17]Qian, M. and Zhang, Z. S. Ergodic theory for Axiom A endomorphisms. Ergodic Th. and Dyn. Syst. vol. 15, no. 1 (1995), 161–174.Google Scholar
[18]Ruelle, D.Elements of Differentiable Dynamics and Bifurcation Theory (Academic Press, 1989).Google Scholar
[19]Tsuji, M.Fat solenoidal attractors. Nonlinearity 14 (2001), 1011–1027.CrossRefGoogle Scholar
[20]Walters, P.An Introduction to Ergodic Theory (Springer-Verlag, 1982).CrossRefGoogle Scholar