Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T01:13:08.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Measure theory over boolean toposes

Published online by Cambridge University Press:  30 August 2016

SIMON HENRY
SIMON HENRY*
Affiliation:
College de france, ATER chair d'analyse et géométrie, 3 Rue d'Ulm, Paris 75005, France e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we develop a notion of measure theory over boolean toposes reminiscent of the theory of von Neumann algebras. This is part of a larger project to study relations between topos theory and noncommutative geometry. The main result is a topos theoretic version of the modular time evolution of von Neumann algebras which take the form of a canonical 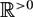$\mathbb{R}^{>0}$-principal bundle over any integrable locally separated boolean topos.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 163 , Issue 1 , July 2017 , pp. 1 - 21
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Ghez, P., Lima, R. and Roberts, J. E W*-categories. Pacific J. Math. 120 (1) (1985), 79–109.Google Scholar
[2] Henry, S. Des topos à la géométrie non commutative par l'étude des espaces de Hilbert internes. PhD thesis. Université Paris 7 (2014).Google Scholar
[3] Henry, S. Toward a non-commutative Gelfand duality: Boolean locally separated toposes and monoidal monotone complete C*-categories. arXiv preprint arXiv:1501.07045 (2015).Google Scholar
[4] Jackson, M. A sheaf theoretic approach to measure theory. PhD thesis. University of Pittsburgh (2006).Google Scholar
[5] Johnstone, P. T. Stone spaces (Cambridge University Press, 1986).Google Scholar
[6] Johnstone, P. T. Sketches of an Elephant: a Topos Theory Compendium (Clarendon Press, 2002).Google Scholar
[7] MacLane, S. and Moerdijk, I. Sheaves in Geometry and Logic: a First Introduction to Topos Theory (Springer, 1992).Google Scholar
[8] Moerdijk, I. and Vermeulen, J. J. C. Proper Maps of Toposes, vol. 705 (AMS Bookstore, 2000).Google Scholar
[9] Saitô, K. and Wright, J. D. M. Monotone complete C*-algebras and generic dynamics. Proc. London Math. Soc. (2013), page pds 084.Google Scholar
[10] Takesaki, M. Theory of Operator Algebras I, vol. 1 (Springer, 2003).Google Scholar
[11] Takesaki, M. Theory of Operator Algebras II, vol. 2 (Springer, 2003).CrossRefGoogle Scholar
[12] Vickers, S. A localic theory of lower and upper integrals. Mathematical Logic Quarterly. 54 (1) (2008), 109–123.Google Scholar