Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T00:58:30.796Z Has data issue: false hasContentIssue false
  • English
  • Français

Means and coefficients of functions which omit a sequence of values

Published online by Cambridge University Press:  24 October 2008

Albert Baernstein II  and
Richard Rochberg
Albert Baernstein II
Affiliation:
Washington University, St Louis, MO, 63130 U.S.A.
Richard Rochberg
Affiliation:
Washington University, St Louis, MO, 63130 U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose that f is analytic in the unit disk D. If its range f(D) is contained in a simply connected proper subdomain of the plane, then the principle of subordination and the distortion theorem for univalent functions show that

where M(r, f) denotes the maximum modulus of f. Cartwright (2) studied functions which, instead of omitting all values on a continuum stretching to infinity, omit only a sequence of values. She assumed that the sequence {wn} satisfies

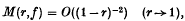
and

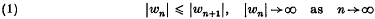
and proved that if f(D) contains none of the points {wn} thenm

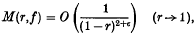
for every ε > 0. Cartwright's proof was based on the Ahlfors Distortion Theorem, and is quite complicated. A much simpler proof was given by Pommerenke in (10). The key idea in his proof will also be used in the present paper.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 81 , Issue 1 , January 1977 , pp. 47 - 57
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baernstein, A.Integral means, univalent functions, and circular symmetrization. Acta Math. 133 (1974), 139–169.CrossRefGoogle Scholar
(2)Cartwright, M. L.Some inequalities in the theory of functions. Math. Ann. 3 (1935), 98–118.CrossRefGoogle Scholar
(3)Duren, P. L.The theory of Hp Spaces (Academic Press, 1970).Google Scholar
(4)Hayman, W. K.Inequalities in the theory of functions. Proc. London Math. Soc. 51 (1949), 450–473.CrossRefGoogle Scholar
(5)Hayman, W. K. Uniformly normal families. Lectures on functions of a complex variable, ed. Kaplan, W. (University of Michigan Press, 1955).Google Scholar
(6)Hayman, W. K.Research problems in function theory (University of London Press, 1967).Google Scholar
(7)Hayman, W. K.Values and growth of functions regular in the unit disk, to appear in the Proceedings of a Conference at University of Kentucky,May 1976,which will be published in the Springer Lecture Notes series.CrossRefGoogle Scholar
(8)Hayman, W. K. and Weitsman, A.On the coefficients and means of functions omitting values. Math. Proc. Cambridge Philos. Soc. 77 (1975), 119–137.CrossRefGoogle Scholar
(9)Nevanlinna, R.Analytic functions (Springer-Verlag, 1970).CrossRefGoogle Scholar
(10)Pommerenke, C.On the growth of the coefficients of analytic functions. J. London Math. Soc. 5 (1972), 624–628.CrossRefGoogle Scholar