Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Weit, Yitzhak
1991.
On a generalized asymptotic mean value property.
Aequationes Mathematicae,
Vol. 41,
Issue. 1,
p.
242.
Netuka, Ivan
and
Veselý, Jiří
1994.
Classical and Modern Potential Theory and Applications.
p.
359.
Trofymenko, O. D.
2011.
Analog of the mean-value theorem for polynomials of special form.
Ukrainian Mathematical Journal,
Vol. 63,
Issue. 5,
p.
815.
Minenkova, Anastasiia
and
Trofimenko, Olga
2019.
Topics in Classical and Modern Analysis.
p.
279.
Trofymenko, Olga
2020.
Mean value theorems for polynomial solutions of linear elliptic equations with constant coefficients in the complex plane.
Ukrainian Mathematical Bulletin,
Vol. 17,
Issue. 4,
p.
594.
Trofymenko, Olga D.
2021.
Mean value theorems for polynomial solutions of linear elliptic equations with constant coefficients in the complex plane.
Journal of Mathematical Sciences,
Vol. 254,
Issue. 3,
p.
439.


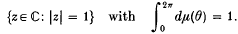
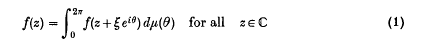
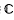 , | ξ | =
, | ξ | = 