Liftings of formal groups and the Artinian completion of 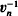 BP
BP
Published online by Cambridge University Press: 24 October 2008
Extract
Let 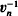 BP denote the localization at υn, of the Brown-Peterson spectrum (associated to the prime p). There is a related ring spectrum E(n) with homotopy ring
BP denote the localization at υn, of the Brown-Peterson spectrum (associated to the prime p). There is a related ring spectrum E(n) with homotopy ring

(as a quotient ring of  in fact the cohomology theory E(n)*( ) is determined via a Conner-Floyd type isomorphism from
in fact the cohomology theory E(n)*( ) is determined via a Conner-Floyd type isomorphism from  on finite complexes, and moreover E(n) and
on finite complexes, and moreover E(n) and 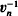 BP are in the same Bousfield class (see [2, 14]). Although it is known (essentially from [17]) that
BP are in the same Bousfield class (see [2, 14]). Although it is known (essentially from [17]) that 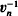 BP cannot be a product of suspensions of E(n) in a multiplicative sense, D. Ravenel conjectured that such a splitting might occur after suitable completion of these spectra (see the introduction to [14]). This question was the original motivation of the present paper; however in proving Ravenel's conjecture we were naturally led to the consideration of some fundamental results in the theory of liftings of formal group laws and ‘change of ring’ results for Ext groups occurring in connection with the work of [10, 11, 12].
BP cannot be a product of suspensions of E(n) in a multiplicative sense, D. Ravenel conjectured that such a splitting might occur after suitable completion of these spectra (see the introduction to [14]). This question was the original motivation of the present paper; however in proving Ravenel's conjecture we were naturally led to the consideration of some fundamental results in the theory of liftings of formal group laws and ‘change of ring’ results for Ext groups occurring in connection with the work of [10, 11, 12].
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 106 , Issue 3 , November 1989 , pp. 511 - 530
- Copyright
- Copyright © Cambridge Philosophical Society 1989
References
REFERENCES
- 6
- Cited by


