Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T01:57:06.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Laminar flow in an axially symmetrical jet of compressible fluid, far from the orifice

Published online by Cambridge University Press:  24 October 2008

D. C. Pack
D. C. Pack
Affiliation:
Department of MathematicsUniversity of Manchester*
Get access Rights & Permissions [Opens in a new window]

Abstract

When the boundary-layer approximations are applied to the laminar flow in an axially symmetrical jet of gas with Prandtl number unity, a particular integral of the equations of motion satisfying the required boundary conditions is found to be 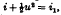, where i1, is the (constant) enthalpy on the jet boundary. By a suitable transformation an equation is obtained which, to a first approximation, may be replaced by the equation for flowin an axially symmetrical jet of incompressible fluid at a sufficiently large distance from the orifice. For an ideal gas, the known solution of this equ`ation may be used as the starting point of an iterative method to build up the stream function as a power series. The next approximation is found explicitly. It shows that for subsonic Mach numbers the density at a point on the axis is greater and the temperature less than on the boundary by amounts which may be very closely represented by terms inversely proportional to the square of the distance of the point from the orifice.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 50 , Issue 1 , January 1954 , pp. 98 - 104
Copyright
Copyright © Cambridge Philosophical Society 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bickley, W.Phil. Mag. (7), 23 (1937), 727.CrossRefGoogle Scholar
(2)Crocco, L.Monogr. sci. Aero., Roma, no. 3 (1946). (Cited in (5) below.)Google Scholar
(3)Goldstein, S. (editor). Modern developments in fluid dynamics, vol. 1 (Oxford, 1938).Google Scholar
(4)Howarth, L.Proc. roy. Soc. A, 194 (1948), 16.Google Scholar
(5)Illingworth, C. R.Proc. roy. Soc. A, 199 (1949), 533.Google Scholar
(6)Kármán, Th. von and Tsien, H. S.J. aero. Sci. 6 (1938), 227.Google Scholar
(7)Pai, S. I.Quart. appl. Math. 10 (1952), 141.CrossRefGoogle Scholar
(8)Schlichting, H.Z. angew. Math. Mech. 13 (1933), 260.CrossRefGoogle Scholar