Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T00:09:38.312Z Has data issue: false hasContentIssue false
  • English
  • Français

The L1-norm of exponential sums in d

Published online by Cambridge University Press:  16 January 2013

GIORGIS PETRIDIS
GIORGIS PETRIDIS*
Affiliation:
Department of Mathematics, University of Rochester, NY 14627, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be a finite set of integers and FA(x) = ∑a∈A exp(2πiax) be its exponential sum. McGehee, Pigno and Smith and Konyagin have independently proved that ∥FA∥1 ≥ c log|A| for some absolute constant c. The lower bound has the correct order of magnitude and was first conjectured by Littlewood. In this paper we present lower bounds on the L1-norm of exponential sums of sets in the d-dimensional grid 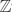d. We show that ∥FA∥1 is considerably larger than log|A| when A ⊂ 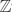d has multidimensional structure. We furthermore prove similar lower bounds for sets in 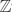, which in a technical sense are multidimensional and discuss their connection to an inverse result on the theorem of McGehee, Pigno and Smith and Konyagin.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 154 , Issue 3 , May 2013 , pp. 381 - 392
Copyright
Copyright © Cambridge Philosophical Society 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balog, A. and Ruzsa, I. Z.A new lower bound for the L 1 mean of exponential sums with the Möbius function. Bull. Lond. Math. Soc. 31 (1999), 415–418.CrossRefGoogle Scholar
[2]Cohen, P. J.On a conjecture of Littlewood and idempotent measures. Amer. J. Math. 82 (1960), 191–212.CrossRefGoogle Scholar
[3]Davenport, H.On a theorem of P. J. Cohen. Mathematika 7 (1960), 93–97.CrossRefGoogle Scholar
[4]Green, B. J. and Sanders, T.Boolean functions with small spectral norm. Geom. Funct. Anal. 18 (1) (2008), 144–162.CrossRefGoogle Scholar
[5]Green, B. J. and Sanders, T.A quantitative version of the idempotent theorem in harmonic analysis. Ann. of Math. (2) 168 (3) (2008), 1025–1054.CrossRefGoogle Scholar
[6]Hardy, G. H. and Littlewood, J. E.A new proof of a theorem on rearrangements. J. Lond. Math. Soc. (2) 23 (1948), 163–168.CrossRefGoogle Scholar
[7]Konyagin, S. V.On the Littlewood problem. Izv. Akad. Nauk SSSR Ser. Mat. 45 (2) (1981), 243–265.Google Scholar
[8]Lorch, L.The principal term in the asymptotic expansion of the Lebesgue constants. Amer. Math. Monthly 61 (1954), 245–249.CrossRefGoogle Scholar
[9]McGehee, O. C., Pigno, L. and Smith, B.Hardy's inequality and the L 1 norm of exponential sums. Ann. of Math.(2) 113 (3) (1981), 613–618.CrossRefGoogle Scholar
[10]Pichorides, S. K.A lower bound for the L 1 norm of exponential sums. Mathematika 21 (1974), 155–159.CrossRefGoogle Scholar
[11]Shao, X. On character sums and exponential sums over generalised arithmetic progressions. Preprint, arXiv:1206.0521v2 (2012).Google Scholar
[12]Vaughan, R. C.The L 1 mean of exponential sums over primes. Bull. Lond. Math. Soc. 20 (2) (1988), 121–123.CrossRefGoogle Scholar