Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T16:35:51.460Z Has data issue: false hasContentIssue false
  • English
  • Français

Isotopy classes of embeddings and homotopy

Published online by Cambridge University Press:  24 October 2008

G. S. Wells
G. S. Wells
Affiliation:
University College of Wales, Aberystwyth
Get access Rights & Permissions [Opens in a new window]

Extract

Haefliger's theorem (3) that the group of isotopy classes of embeddings of Sx in Sn when n − x > 2 is isomorphic to the triad group πx+1(G; G(n − x),SO), where G(n − x) is the H-space of homotopy equivalences of Sn−x−1 of degree 1, 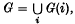, and SO is the stable special orthogonal group, is generalized in this paper by replacing Sx and Sn by arbitrary compact connected smooth manifolds Xx, Mn without boundary. The embedding and knot problems are reduced to homotopy theory. The question of P.L. manifolds is discussed in section 4. The case Mn = Sn will be considered first; the generalization is stated in section 3.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 1 , July 1969 , pp. 21 - 26
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Armstrong, M. A.Transversality for polyhedra. Ann. of Math. 86 (1967), 172–191.CrossRefGoogle Scholar
(2)Browder, W.Embedding 1-connected manifolds. Bull. Amer. Math. Soc. 72 (1966), 225–231.CrossRefGoogle Scholar
(3)Haefliger, A.Differentiable embeddings of S n in S n+q for q > 2. Ann. of Math. 83 (1966), 402–436.CrossRefGoogle Scholar
(4)Hudson, J.Unpublished sequel to Piecewize linear embeddings. Ann. of Math. 85 (1967), 1–31.CrossRefGoogle Scholar
(5)Williamson, R. E. Jr. Cobordism of combinatorial manifolds. Ann. of Math. 83 (1966), 1–83.CrossRefGoogle Scholar
(6)Rourke, C. P. and Sanderson, B. J.Block bundles: II. Transversality. Ann. of Math. 87 (1968), 256–278.CrossRefGoogle Scholar