Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T01:24:37.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Irredundant families of subcubes

Published online by Cambridge University Press:  12 January 2011

DAVID ELLIS
DAVID ELLIS*
Affiliation:
St John's College, Cambridge. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the problem of finding the maximum possible size of a family of d-dimensional subcubes of the n-cube {0, 1}n, none of which is contained in the union of the others. (We call such a family ‘irredundant’). Aharoni and Holzman [1] conjectured that for d > n/2, the answer is (which is attained by the family of all d-subcubes containing a fixed point). We prove this in the case where all the subcubes go through either (0, 0, . . . , 0) or (1, 1, . . . , 1). We also give a new proof of an upper bound of Meshulam [6]. Finally, we consider the case d ≤ n/2. We give a probabilistic construction showing that in this case, Meshulam's upper bound is correct to within a constant factor. When n = 2d, we construct an irredundant family of size .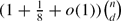

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 150 , Issue 2 , March 2011 , pp. 257 - 272
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aharoni, R. and Holzman, R. Oberwolfach, 1991.Google Scholar
[2]Babai, L. and Frankl, P. Linear algebra methods in combinatorics with applications to geometry and computer science. Preprint, 1992.Google Scholar
[3]Bollobás, B. Combinatorics: Set Systems, Hypergraphs, Families of Vectors, and Combinatorial Probability. (Cambridge University Press, 1986).Google Scholar
[4]Corrádi, K. A. and Katai, I.A note on combinatorics. Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 12 (1969), 100–106.Google Scholar
[5]Kabatyanskii, G. A. and Panchenko, V. I.Unit sphere packings and coverings of the hamming space. Probl. Inf. Transm. 24 (1988), 261–272.Google Scholar
[6]Meshulam, R.On families of faces in discrete cubes. Graphs Combin. 8 (1992), 287–289.CrossRefGoogle Scholar
[7]Tietäväinen, A.On the nonexistence of perfect codes over finite fields. SIAM J. Appl. Math. 24 (1973).CrossRefGoogle Scholar