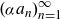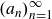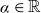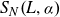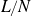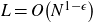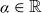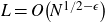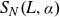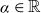1. Introduction
A real-valued sequence
![]() $\left(x_{n}\right)_{n=1}^{\infty}$
is said to be uniformly distributed (or equidistributed) modulo one if, for every interval
$\left(x_{n}\right)_{n=1}^{\infty}$
is said to be uniformly distributed (or equidistributed) modulo one if, for every interval
![]() $I\subseteq[0,1)$
, we have
$I\subseteq[0,1)$
, we have
where
![]() $\left\{ x\right\} $
denotes the fractional part of x, and
$\left\{ x\right\} $
denotes the fractional part of x, and
![]() $\left|I\right|$
denotes the length of the interval I. There are many examples of sequences which satisfy this property, e.g., the Kronecker sequence
$\left|I\right|$
denotes the length of the interval I. There are many examples of sequences which satisfy this property, e.g., the Kronecker sequence
![]() $x_{n}=\alpha n$
where
$x_{n}=\alpha n$
where
![]() $\alpha$
is irrational, and more generally (as was shown by Weyl in his pioneering 1916 paper [
Reference Weyl18
]) the sequence
$\alpha$
is irrational, and more generally (as was shown by Weyl in his pioneering 1916 paper [
Reference Weyl18
]) the sequence
![]() $x_{n}=\alpha_{d}n^{d}+\dots+\alpha_{1}n+\alpha_{0}$
(
$x_{n}=\alpha_{d}n^{d}+\dots+\alpha_{1}n+\alpha_{0}$
(
![]() $\alpha_{i}\in\mathbb{R}$
), where at least one of the coefficients
$\alpha_{i}\in\mathbb{R}$
), where at least one of the coefficients
![]() $\alpha_{1},\dots,\alpha_{d}$
is irrational. In the metric sense, more can be said: Weyl proved [
Reference Weyl18
] that for any sequence
$\alpha_{1},\dots,\alpha_{d}$
is irrational. In the metric sense, more can be said: Weyl proved [
Reference Weyl18
] that for any sequence
![]() $\left(a_{n}\right)_{n=1}^{\infty}$
of distinct integers, the sequence
$\left(a_{n}\right)_{n=1}^{\infty}$
of distinct integers, the sequence
![]() $x_{n}=\alpha a_{n}$
is uniformly distributed modulo one for (Lebesgue) almost all
$x_{n}=\alpha a_{n}$
is uniformly distributed modulo one for (Lebesgue) almost all
![]() $\alpha\in\mathbb{R}$
. This is also true for real-valued sequences whose elements are sufficiently separated from each other (see, e.g., [
Reference Kuipers and Niederreiter6
, chapter 1, corollary 4·1]): if
$\alpha\in\mathbb{R}$
. This is also true for real-valued sequences whose elements are sufficiently separated from each other (see, e.g., [
Reference Kuipers and Niederreiter6
, chapter 1, corollary 4·1]): if
![]() $\left(a_{n}\right)_{n=1}^{\infty}$
is a real-valued sequence, and there exists a positive constant
$\left(a_{n}\right)_{n=1}^{\infty}$
is a real-valued sequence, and there exists a positive constant
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\left|a_{n}-a_{m}\right|\ge\delta$
for each
$\left|a_{n}-a_{m}\right|\ge\delta$
for each
![]() $n\ne m$
, then the sequence
$n\ne m$
, then the sequence
![]() $x_{n}=\alpha a_{n}$
is uniformly distributed modulo one for almost all
$x_{n}=\alpha a_{n}$
is uniformly distributed modulo one for almost all
![]() $\alpha\in\mathbb{R}$
. This condition clearly holds for real-valued, positive, lacunary sequences, i.e., sequences such that
$\alpha\in\mathbb{R}$
. This condition clearly holds for real-valued, positive, lacunary sequences, i.e., sequences such that
![]() $a_{1}>0$
, and there exists a constant
$a_{1}>0$
, and there exists a constant
![]() $C>1$
such that for all
$C>1$
such that for all
![]() $n\ge1$
we have
$n\ge1$
we have
While the classical theory deals with the distribution of sequences modulo one at “large” scales, there has been a growing interest in recent years in the fluctuations of sequences at smaller scales. For many sequences, it is conjectured (backed up by numerical evidence) that the small-scale statistics (at the scale
![]() $1/N$
– the mean gap of the first N elements of the sequence modulo one) are in agreement with the statistics of uniform i.i.d. random points in the unit interval (Poissonian statistics), thus demonstrating pseudo-random behaviour for such sequences. The rigorous study of such questions was initiated by Rudnick and Sarnak [
Reference Rudnick and Sarnak13
], who considered the pair correlation (see (1·3), with L fixed) of the sequence
$1/N$
– the mean gap of the first N elements of the sequence modulo one) are in agreement with the statistics of uniform i.i.d. random points in the unit interval (Poissonian statistics), thus demonstrating pseudo-random behaviour for such sequences. The rigorous study of such questions was initiated by Rudnick and Sarnak [
Reference Rudnick and Sarnak13
], who considered the pair correlation (see (1·3), with L fixed) of the sequence
![]() $ x_n = \alpha n^d$
modulo one (
$ x_n = \alpha n^d$
modulo one (
![]() $ d\ge 2 $
), and proved Poissonian limiting behaviour for almost all
$ d\ge 2 $
), and proved Poissonian limiting behaviour for almost all
![]() $ \alpha \in \mathbb{R} $
; while the same limiting behaviour is conjectured to hold for any specific irrational
$ \alpha \in \mathbb{R} $
; while the same limiting behaviour is conjectured to hold for any specific irrational
![]() $ \alpha $
which is badly approximable by rationals, the question remains open, as are most questions about small-scale statistics of specific sequences (i.e., not in the metric sense).
$ \alpha $
which is badly approximable by rationals, the question remains open, as are most questions about small-scale statistics of specific sequences (i.e., not in the metric sense).
A popular small-scale statistic is the (normalised) gap distribution of the re-ordered first N elements of the sequence modulo one, which for many sequences is expected to converge to the exponential distribution (“Poissonian gap statistics”) – the almost sure limiting distribution of the gaps in the random model. Lacunary sequences are among the rare examples where such behaviour has been rigorously proved to hold (in the metric sense): Rudnick and Zaharescu proved [
Reference Rudnick and Zaharescu16
] Poissonian gap statistics for almost all
![]() $\alpha\in\mathbb{R}$
for the sequence
$\alpha\in\mathbb{R}$
for the sequence
![]() $x_{n}=\alpha a_{n}$
where
$x_{n}=\alpha a_{n}$
where
![]() $\left(a_{n}\right)_{n=1}^{\infty}$
is an integer-valued lacunary sequence; this was recently extended to real-valued lacunary sequences by Chaubey and the author [
Reference Chaubey and Yesha2
]. At the other extreme, Lutsko and Technau recently proved [
Reference Lutsko and Technau10
] Poissonian gap statistics for the slowly growing sequence
$\left(a_{n}\right)_{n=1}^{\infty}$
is an integer-valued lacunary sequence; this was recently extended to real-valued lacunary sequences by Chaubey and the author [
Reference Chaubey and Yesha2
]. At the other extreme, Lutsko and Technau recently proved [
Reference Lutsko and Technau10
] Poissonian gap statistics for the slowly growing sequence
![]() $ x_n = \alpha (\log n)^A$
(
$ x_n = \alpha (\log n)^A$
(
![]() $ A>1 $
) – remarkably, this holds for any
$ A>1 $
) – remarkably, this holds for any
![]() $ \alpha>0 $
, and not only in the metric sense – see also the closely related results [
Reference Lutsko, Sourmelidis and Technau8, Reference Lutsko and Technau9
] about Poissonian correlations for the sequence
$ \alpha>0 $
, and not only in the metric sense – see also the closely related results [
Reference Lutsko, Sourmelidis and Technau8, Reference Lutsko and Technau9
] about Poissonian correlations for the sequence
![]() $ x_n = \alpha n^\theta $
where
$ x_n = \alpha n^\theta $
where
![]() $ \theta $
is small.
$ \theta $
is small.
Statistics in the “mesoscopic” regime, i.e., at the scale
![]() $L/N$
, where
$L/N$
, where
![]() $L=L\!\left(N\right)\to\infty$
and
$L=L\!\left(N\right)\to\infty$
and
![]() $L=o\!\left(N\right)$
as
$L=o\!\left(N\right)$
as
![]() $N\to\infty$
, provide further information which may capture some interesting features of sequences. An example of such a statistic is the number variance (the variance of the number of elements in random intervals, see the definition below in our setting), famously studied for the zeros of the Riemann zeta function, for which at small scales the number variance is consistent with that of the eigenvalues of random matrices drawn from the Gaussian unitary ensemble (GUE), whereas “saturation” occurs at larger scales (see [
Reference Berry1
]). In the context of sequences modulo one, only a few results have been established so far in the mesoscopic regime, mainly concerning the leading order asymptotics of the long-range correlations of the sequence
$N\to\infty$
, provide further information which may capture some interesting features of sequences. An example of such a statistic is the number variance (the variance of the number of elements in random intervals, see the definition below in our setting), famously studied for the zeros of the Riemann zeta function, for which at small scales the number variance is consistent with that of the eigenvalues of random matrices drawn from the Gaussian unitary ensemble (GUE), whereas “saturation” occurs at larger scales (see [
Reference Berry1
]). In the context of sequences modulo one, only a few results have been established so far in the mesoscopic regime, mainly concerning the leading order asymptotics of the long-range correlations of the sequence
![]() $x_{n}=\alpha n^{2}$
(see [
Reference Heath–Brown4, Reference Hille5, Reference Lutsko7, Reference Nair and Pollicott12, Reference Technau and Walker17
]); nevertheless, important intermediate-scale statistics such as the number variance have largely remained unexplored. The aim of this paper is to study such statistics for real-valued lacunary sequences.
$x_{n}=\alpha n^{2}$
(see [
Reference Heath–Brown4, Reference Hille5, Reference Lutsko7, Reference Nair and Pollicott12, Reference Technau and Walker17
]); nevertheless, important intermediate-scale statistics such as the number variance have largely remained unexplored. The aim of this paper is to study such statistics for real-valued lacunary sequences.
Let
![]() $\left(a_{n}\right)_{n=1}^{\infty}$
be a positive, real-valued lacunary sequence; we are interested in the distribution of the number of elements modulo one of the sequence
$\left(a_{n}\right)_{n=1}^{\infty}$
be a positive, real-valued lacunary sequence; we are interested in the distribution of the number of elements modulo one of the sequence
![]() $\left(x_{n}\right)_{n=1}^{\infty}=\left(\alpha a_{n}\right)_{n=1}^{\infty}$
in intervals of length
$\left(x_{n}\right)_{n=1}^{\infty}=\left(\alpha a_{n}\right)_{n=1}^{\infty}$
in intervals of length
![]() $L/N$
around points
$L/N$
around points
![]() $x\in[0,1)$
, which we denote by
$x\in[0,1)$
, which we denote by
 \begin{align*}S_{N}\!\left(L,\alpha\right)=S_{N}\!\left(L,\alpha\right)\left(x\right)\;:\!=\;\sum_{j=1}^{N}\sum_{n\in\mathbb{Z}}\chi\!\left(\frac{\alpha a_{j}-x+n}{L/N}\right)\!,\end{align*}
\begin{align*}S_{N}\!\left(L,\alpha\right)=S_{N}\!\left(L,\alpha\right)\left(x\right)\;:\!=\;\sum_{j=1}^{N}\sum_{n\in\mathbb{Z}}\chi\!\left(\frac{\alpha a_{j}-x+n}{L/N}\right)\!,\end{align*}
where
![]() $\chi=\chi_{\left[-1/2,1/2\right]}$
is the characteristic function of the interval
$\chi=\chi_{\left[-1/2,1/2\right]}$
is the characteristic function of the interval
![]() $\left[-1/2,1/2\right]$
.
$\left[-1/2,1/2\right]$
.
The first statistic that we will study is the number variance
i.e., the variance of
![]() $S_{N}\!\left(L,\alpha\right)$
, where we randomise w.r.t. the centre of the interval x. We would like to show that for generic values of
$S_{N}\!\left(L,\alpha\right)$
, where we randomise w.r.t. the centre of the interval x. We would like to show that for generic values of
![]() $\alpha\in\mathbb{R}$
, we have
$\alpha\in\mathbb{R}$
, we have
which is in agreement with the random model. In our first main result we show that (1·1) holds with high probability in (essentially) the full mesoscopic regime (namely, all the way up to
![]() $L=O\!\left(N^{1-\epsilon}\right)$
where
$L=O\!\left(N^{1-\epsilon}\right)$
where
![]() $\epsilon$
is arbitrarily small).
$\epsilon$
is arbitrarily small).
Theorem 1·1.
Let
![]() $\epsilon>0$
, and let I be a bounded interval. Assume that
$\epsilon>0$
, and let I be a bounded interval. Assume that
![]() $L=L\!\left(N\right)=O\!\left(N^{1-\epsilon}\right)$
as
$L=L\!\left(N\right)=O\!\left(N^{1-\epsilon}\right)$
as
![]() $N\to\infty$
. Then (1·1) holds with high probability w.r.t.
$N\to\infty$
. Then (1·1) holds with high probability w.r.t.
![]() $\alpha$
: for any
$\alpha$
: for any
![]() $\delta>0$
, we have
$\delta>0$
, we have
as
![]() $N\to\infty$
.
$N\to\infty$
.
It is desirable to extend this to an almost sure statement, which we are able to establish in a narrower regime
![]() $L=O\!\left(N^{1/2-\epsilon}\right)$
(along with a technical condition on the oscillations of L, which clearly holds for natural choices of L, e.g., when
$L=O\!\left(N^{1/2-\epsilon}\right)$
(along with a technical condition on the oscillations of L, which clearly holds for natural choices of L, e.g., when
![]() $L=N^{s}$
with
$L=N^{s}$
with
![]() $s\le1/2-\epsilon$
).
$s\le1/2-\epsilon$
).
Theorem 1·2.
Let
![]() $\epsilon>0$
, and assume that
$\epsilon>0$
, and assume that
![]() $L=L\!\left(N\right)=O\!\left(N^{1/2-\epsilon}\right)$
and that
$L=L\!\left(N\right)=O\!\left(N^{1/2-\epsilon}\right)$
and that
![]() $L\!\left(N+1\right)-L\!\left(N\right)=o\!\left(N^{-1/2}\right)$
as
$L\!\left(N+1\right)-L\!\left(N\right)=o\!\left(N^{-1/2}\right)$
as
![]() $N\to\infty$
. Then for almost all
$N\to\infty$
. Then for almost all
![]() $\alpha\in\mathbb{R}$
, we have
$\alpha\in\mathbb{R}$
, we have
as
![]() $N\to\infty$
.
$N\to\infty$
.
For slowly growing L (and under an even milder condition on its oscillations), we will be able to establish a central limit theorem for
![]() $S_{N}\!\left(L,\alpha\right)$
. This would hold for example when
$S_{N}\!\left(L,\alpha\right)$
. This would hold for example when
![]() $L=\left(\log N\right)^{t}$
with
$L=\left(\log N\right)^{t}$
with
![]() $t>0$
.
$t>0$
.
Theorem 1·3.
Let
![]() $L=L\!\left(N\right)\to\infty$
as
$L=L\!\left(N\right)\to\infty$
as
![]() $N\to\infty$
such that for all
$N\to\infty$
such that for all
![]() $\eta>0$
we have
$\eta>0$
we have
![]() $L=O\!\left(N^{\eta}\right)$
, and assume that there exists
$L=O\!\left(N^{\eta}\right)$
, and assume that there exists
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
![]() $L\!\left(N+1\right)-L\!\left(N\right)=O\!\left(N^{-\epsilon}\right)$
. Then for almost all
$L\!\left(N+1\right)-L\!\left(N\right)=O\!\left(N^{-\epsilon}\right)$
. Then for almost all
![]() $\alpha\in\mathbb{R}$
, for any
$\alpha\in\mathbb{R}$
, for any
![]() $a<b$
, we have
$a<b$
, we have
as
![]() $N\to\infty$
.
$N\to\infty$
.
We remark that while the condition
![]() $L\!\left(N\right)\to\infty$
in Theorem 1·3 is essential, Theorems 1·1 and 1·2 also hold for fixed L, thus extending the results of [
Reference Rudnick and Technau14
].
$L\!\left(N\right)\to\infty$
in Theorem 1·3 is essential, Theorems 1·1 and 1·2 also hold for fixed L, thus extending the results of [
Reference Rudnick and Technau14
].
We would like to stress the difference between (1·1) and some weaker notions of long-range Poissonian correlations, as studied, e.g., in [
Reference Hille5, Reference Lutsko7, Reference Technau and Walker17
]. Note that the number variance
![]() $\Sigma_{N}^{2}\!\left(L,\alpha\right)$
can be expressed in terms of the pair correlation function. Indeed, a direct calculation shows (see, e.g., [
Reference Marklof11
]) that
$\Sigma_{N}^{2}\!\left(L,\alpha\right)$
can be expressed in terms of the pair correlation function. Indeed, a direct calculation shows (see, e.g., [
Reference Marklof11
]) that
where
 \begin{equation}R_{N}^{2}\!\left(L,\alpha,\Delta\right)=\frac{1}{N}\sum_{i\ne j=1}^{N}\sum_{n\in\mathbb{Z}}\Delta\!\left(\frac{\alpha a_{i}-\alpha a_{j}+n}{L/N}\right)\end{equation}
\begin{equation}R_{N}^{2}\!\left(L,\alpha,\Delta\right)=\frac{1}{N}\sum_{i\ne j=1}^{N}\sum_{n\in\mathbb{Z}}\Delta\!\left(\frac{\alpha a_{i}-\alpha a_{j}+n}{L/N}\right)\end{equation}
is the (scaled) pair correlation function of
![]() $\left(\alpha a_{n}\right)_{n=1}^{\infty}$
with respect to the test function
$\left(\alpha a_{n}\right)_{n=1}^{\infty}$
with respect to the test function
Hence, (1·1) is equivalent to
We thus see that (1·4), and therefore (1·1), is a significantly stronger statement then long-range Poissonian pair correlation in the sense of
![]() $R_{N}^{2}\!\left(L,\alpha,\Delta\right)=L+o\!\left(L\right)$
, where the error term is insufficient for determining the asymptotics of the number variance. Similarly, for
$R_{N}^{2}\!\left(L,\alpha,\Delta\right)=L+o\!\left(L\right)$
, where the error term is insufficient for determining the asymptotics of the number variance. Similarly, for
![]() $k\ge2$
, consider the k-level correlation function
$k\ge2$
, consider the k-level correlation function
 \begin{equation}R_{N}^{k}\!\left(L,\alpha,\Delta\right)=\frac{1}{N}\sum_{\substack{j_{1},\dots,j_{k}=1\\ \mathrm{distinct}}}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\Delta\!\left(\frac{\alpha a_{j_{1}}-\alpha a_{j_{k}}+n_{1}}{L/N},\dots,\frac{\alpha a_{j_{k-1}}-\alpha a_{j_{k}}+n_{k-1}}{L/N}\right)\!;\end{equation}
\begin{equation}R_{N}^{k}\!\left(L,\alpha,\Delta\right)=\frac{1}{N}\sum_{\substack{j_{1},\dots,j_{k}=1\\ \mathrm{distinct}}}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\Delta\!\left(\frac{\alpha a_{j_{1}}-\alpha a_{j_{k}}+n_{1}}{L/N},\dots,\frac{\alpha a_{j_{k-1}}-\alpha a_{j_{k}}+n_{k-1}}{L/N}\right)\!;\end{equation}
Proposition 4·1, which is the main ingredient in the proof of Theorem 1·3, is notably stronger than long-range Poissonian higher correlations in the sense of
![]() $R_{N}^{k}\!\left(L,\alpha,\Delta\right)=L^{k}+o\!\left(L^{k}\right)$
, which would be insufficient for concluding Theorem 1·3.
$R_{N}^{k}\!\left(L,\alpha,\Delta\right)=L^{k}+o\!\left(L^{k}\right)$
, which would be insufficient for concluding Theorem 1·3.
2. The number variance
By the Poisson summation formula, we have the following identity for the pair correlation function (1·3)
where
 \begin{align*}T_{N}\!\left(L,\alpha\right)=\frac{L}{N^{2}}\sum_{i\ne j=1}^{N}\sum_{0\ne n\in\mathbb{Z}}\widehat{\Delta}\!\left(\frac{nL}{N}\right)e\!\left(n\alpha\left(a_{i}-a_{j}\right)\right)\end{align*}
\begin{align*}T_{N}\!\left(L,\alpha\right)=\frac{L}{N^{2}}\sum_{i\ne j=1}^{N}\sum_{0\ne n\in\mathbb{Z}}\widehat{\Delta}\!\left(\frac{nL}{N}\right)e\!\left(n\alpha\left(a_{i}-a_{j}\right)\right)\end{align*}
with
(we have used the standard notation
![]() $e\!\left(z\right)=e^{2\pi iz}).$
$e\!\left(z\right)=e^{2\pi iz}).$
We fix a smooth, compactly supported, non-negative weight function
![]() $\rho\in C_{c}^{\infty}\left(\mathbb{R}\right)\!,\,\rho\ge0$
, and denote the weighted
$\rho\in C_{c}^{\infty}\left(\mathbb{R}\right)\!,\,\rho\ge0$
, and denote the weighted
![]() $L^{2}-$
norm of
$L^{2}-$
norm of
![]() $T_{n}\left(L,\alpha\right)$
by
$T_{n}\left(L,\alpha\right)$
by
 \begin{align*}V_{N}\!\left(L\right) & =\int\left|T_{N}\!\left(L,\alpha\right)\right|^{2}\rho\!\left(\alpha\right)\,d\alpha=\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne n_{1}\in\mathbb{Z}\\ 0\ne n_{2}\in\mathbb{Z}}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)w\!\left(n_{1},n_{_{2}},N\right)\!,\end{align*}
\begin{align*}V_{N}\!\left(L\right) & =\int\left|T_{N}\!\left(L,\alpha\right)\right|^{2}\rho\!\left(\alpha\right)\,d\alpha=\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne n_{1}\in\mathbb{Z}\\ 0\ne n_{2}\in\mathbb{Z}}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)w\!\left(n_{1},n_{_{2}},N\right)\!,\end{align*}
where
 \begin{align*}w\!\left(n_{1},n_{_{2}},N\right)=\sum_{\substack{1\le x_{1}\ne y_{1}\le N\\ 1\le x_{2}\ne y_{2}\le N}}\widehat{\rho}\left(n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)\right)\!;\end{align*}
\begin{align*}w\!\left(n_{1},n_{_{2}},N\right)=\sum_{\substack{1\le x_{1}\ne y_{1}\le N\\ 1\le x_{2}\ne y_{2}\le N}}\widehat{\rho}\left(n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)\right)\!;\end{align*}
the aim of the rest of this section is to give an upper bound for
![]() $V_{N}\!\left(L\right)$
.
$V_{N}\!\left(L\right)$
.
We first observe the following identity which will be useful for estimating sums involving
![]() $\widehat{\Delta}$
.
$\widehat{\Delta}$
.
Lemma 2·1. Let
![]() $1\le L<N$
. We have
$1\le L<N$
. We have
Proof. Let
![]() $\Delta_{N/L}\left(x\right)=\Delta\!\left(\frac{N}{L}x\right)$
. By the Poisson summation formula we have
$\Delta_{N/L}\left(x\right)=\Delta\!\left(\frac{N}{L}x\right)$
. By the Poisson summation formula we have
In the next lemma, we will see that up to an error term of order
![]() $O\!\left(N^{-1}\right)\!,$
the ranges of the summations defining
$O\!\left(N^{-1}\right)\!,$
the ranges of the summations defining
![]() $V_{N}\!\left(L\right)$
can be significantly restricted.
$V_{N}\!\left(L\right)$
can be significantly restricted.
Lemma 2·2.
Let
![]() $1\le L<N$
and let
$1\le L<N$
and let
![]() $\epsilon > 0$
We have
$\epsilon > 0$
We have
 \begin{align*}V_{N}\!\left(L\right) & =\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne\left|n_{1}\right|\le N^{4}\\ 0\ne\left|n_{2}\right|\le N^{4}}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)\tilde{w}\!\left(n_{1},n_{2},N\right)+O\!\left(N^{-1}\right)\!,\end{align*}
\begin{align*}V_{N}\!\left(L\right) & =\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne\left|n_{1}\right|\le N^{4}\\ 0\ne\left|n_{2}\right|\le N^{4}}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)\tilde{w}\!\left(n_{1},n_{2},N\right)+O\!\left(N^{-1}\right)\!,\end{align*}
where
 \begin{align*}\tilde{w}\!\left(n_{1},n_{2},N\right)=\sum_{\substack{1\le x_{1}\ne y_{1}\le N\\ 1\le x_{2}\ne y_{2}\le N\\ \max\left\{ x_{1},x_{2},y_{1},y_{2}\right\} >N^{1/4}\\ \left|n_{1}\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\left(a_{x_{2}}-a_{y_{2}}\right)\right|\le N^{\epsilon}}}\widehat{\rho}\left(n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)\right)\!.\end{align*}
\begin{align*}\tilde{w}\!\left(n_{1},n_{2},N\right)=\sum_{\substack{1\le x_{1}\ne y_{1}\le N\\ 1\le x_{2}\ne y_{2}\le N\\ \max\left\{ x_{1},x_{2},y_{1},y_{2}\right\} >N^{1/4}\\ \left|n_{1}\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\left(a_{x_{2}}-a_{y_{2}}\right)\right|\le N^{\epsilon}}}\widehat{\rho}\left(n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)\right)\!.\end{align*}
Proof. We have
 \begin{gather*}w\!\left(n_{1},n_{_{2}},N\right)-\tilde{w}\!\left(n_{1},n_{2},N\right)\ll\sum_{\substack{x_{1}\ne y_{1}\ge1\\ x_{2}\ne y_{2}\ge1\\ \max\left\{ x_{1},x_{2},y_{1},y_{2}\right\} \le N^{1/4}}}\left|\widehat{\rho}\left(n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)\right)\right|\\[5pt] +\sum_{\substack{1\le x_{1}\ne y_{1}\le N\\ 1\le x_{2}\ne y_{2}\le N\\ \left|n_{1}\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\left(a_{x_{2}}-a_{y_{2}}\right)\right|>N^{\epsilon}}}\left|\widehat{\rho}\left(n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)\right)\right|\ll N,\end{gather*}
\begin{gather*}w\!\left(n_{1},n_{_{2}},N\right)-\tilde{w}\!\left(n_{1},n_{2},N\right)\ll\sum_{\substack{x_{1}\ne y_{1}\ge1\\ x_{2}\ne y_{2}\ge1\\ \max\left\{ x_{1},x_{2},y_{1},y_{2}\right\} \le N^{1/4}}}\left|\widehat{\rho}\left(n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)\right)\right|\\[5pt] +\sum_{\substack{1\le x_{1}\ne y_{1}\le N\\ 1\le x_{2}\ne y_{2}\le N\\ \left|n_{1}\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\left(a_{x_{2}}-a_{y_{2}}\right)\right|>N^{\epsilon}}}\left|\widehat{\rho}\left(n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)\right)\right|\ll N,\end{gather*}
where we bounded the first summation using the bound
![]() $\widehat{\rho}\ll1$
and the second summation using
$\widehat{\rho}\ll1$
and the second summation using
![]() $\widehat{\rho}\left(x\right)\ll x^{-k}$
for all
$\widehat{\rho}\left(x\right)\ll x^{-k}$
for all
![]() $k>0$
. Thus,
$k>0$
. Thus,
 \begin{align*}\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne n_{1}\in\mathbb{Z}\\ 0\ne n_{2}\in\mathbb{Z}}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)\!\left(w\!\left(n_{1},n_{_{2}},N\right)-\tilde{w}\!\left(n_{1},n_{2},N\right)\right) & \ll\frac{L^{2}}{N^{3}}\left(\sum_{n\in\mathbb{Z}}\widehat{\Delta}\!\left(\frac{nL}{N}\right)\!\right)^{2}=\frac{1}{N},\end{align*}
\begin{align*}\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne n_{1}\in\mathbb{Z}\\ 0\ne n_{2}\in\mathbb{Z}}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)\!\left(w\!\left(n_{1},n_{_{2}},N\right)-\tilde{w}\!\left(n_{1},n_{2},N\right)\right) & \ll\frac{L^{2}}{N^{3}}\left(\sum_{n\in\mathbb{Z}}\widehat{\Delta}\!\left(\frac{nL}{N}\right)\!\right)^{2}=\frac{1}{N},\end{align*}
where in the last equality we used Lemma 2·1. Finally, by bounding
![]() $\tilde{w}$
trivially and applying the bound
$\tilde{w}$
trivially and applying the bound
![]() $\widehat{\Delta}\!\left(x\right)\ll x^{-2}$
, we have
$\widehat{\Delta}\!\left(x\right)\ll x^{-2}$
, we have
 \begin{gather*}\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne n_{1}\in\mathbb{Z}\\ 0\ne n_{2}\in\mathbb{Z}\\ \max\left\{ \left|n_{1}\right|,\left|n_{2}\right|\right\} >N^{4}}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)\tilde{w}\!\left(n_{1},n_{2},N\right)\ll L^{2}\sum_{m>N^{4}}\widehat{\Delta}\!\left(\frac{mL}{N}\right)\sum_{n\in\mathbb{Z}}\widehat{\Delta}\!\left(\frac{nL}{N}\right)\\[5pt] =NL\sum_{m>N^{4}}\widehat{\Delta}\!\left(\frac{mL}{N}\right)\ll\frac{N^{3}}{L}\sum_{m>N^{4}}m^{-2}\ll\frac{1}{LN}\end{gather*}
\begin{gather*}\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne n_{1}\in\mathbb{Z}\\ 0\ne n_{2}\in\mathbb{Z}\\ \max\left\{ \left|n_{1}\right|,\left|n_{2}\right|\right\} >N^{4}}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)\tilde{w}\!\left(n_{1},n_{2},N\right)\ll L^{2}\sum_{m>N^{4}}\widehat{\Delta}\!\left(\frac{mL}{N}\right)\sum_{n\in\mathbb{Z}}\widehat{\Delta}\!\left(\frac{nL}{N}\right)\\[5pt] =NL\sum_{m>N^{4}}\widehat{\Delta}\!\left(\frac{mL}{N}\right)\ll\frac{N^{3}}{L}\sum_{m>N^{4}}m^{-2}\ll\frac{1}{LN}\end{gather*}
which concludes the proof.
We will now analyse when the summation defining
![]() $\tilde{w}$
does not vanish.
$\tilde{w}$
does not vanish.
Proposition 2·3.
Fix
![]() $n_{1}$
such that
$n_{1}$
such that
![]() $0<\left|n_{1}\right|\le N^{4}$
, and
$0<\left|n_{1}\right|\le N^{4}$
, and
![]() $x_{1},y_{1}$
such that
$x_{1},y_{1}$
such that
![]() $1\le y_{1}<x_{1}\le N$
,
$1\le y_{1}<x_{1}\le N$
,
![]() $x_{1}>N^{1/4}$
. Then there exist at most
$x_{1}>N^{1/4}$
. Then there exist at most
![]() $O\!\left(N^{\epsilon}\log N\right)$
values of
$O\!\left(N^{\epsilon}\log N\right)$
values of
![]() $n_{2},x_{2},y_{2}$
such that
$n_{2},x_{2},y_{2}$
such that
![]() $0<\left|n_{2}\right|\le N^{4}$
,
$0<\left|n_{2}\right|\le N^{4}$
,
![]() $x_{2}\le x_{1},$
$x_{2}\le x_{1},$
![]() $1\le y_{2}<x_{2}\le N$
, and
$1\le y_{2}<x_{2}\le N$
, and
Proof. We follow the ideas of [ Reference Rudnick and Technau14, Reference Rudnick and Zaharescu15 ]. We have
on the other hand,
Applying the reverse triangle inequality to (2·2), we have
substituting the estimates (2·3) and (2·4), we obtain
Since
![]() $x_{1}>N^{1/4}$
, we have
$x_{1}>N^{1/4}$
, we have
![]() $a_{x_{1}}\ge a_{1}C^{x_{1}-1}>a_{1}C^{N^{1/4}-1}$
, and hence
$a_{x_{1}}\ge a_{1}C^{x_{1}-1}>a_{1}C^{N^{1/4}-1}$
, and hence
and therefore for sufficiently large N we have
so that
![]() $x_{1}-x_{2}\ll\log N$
. Thus, there are at most
$x_{1}-x_{2}\ll\log N$
. Thus, there are at most
![]() $O\!\left(\log N\right)$
possible values for
$O\!\left(\log N\right)$
possible values for
![]() $x_{2}$
, and moreover we conclude that
$x_{2}$
, and moreover we conclude that
![]() $x_{2}\gg N^{1/4}$
, and hence
$x_{2}\gg N^{1/4}$
, and hence
![]() $a_{x_{2}}\gg C^{N^{1/4}}.$
$a_{x_{2}}\gg C^{N^{1/4}}.$
We now fix
![]() $x_{2}$
. Since
$x_{2}$
. Since
 \begin{align*}\left|n_{2}-n_{1}\frac{a_{x_{1}}-a_{y_{1}}}{a_{x_{2}}-a_{y_{2}}}\right|\le\frac{N^{\epsilon}}{a_{x_{2}}-a_{y_{2}}}\le\frac{N^{\epsilon}}{\left(1-\frac{1}{C}\right)a_{x_{2}}}\ll\frac{N^{\epsilon}}{C^{N^{1/4}}},\end{align*}
\begin{align*}\left|n_{2}-n_{1}\frac{a_{x_{1}}-a_{y_{1}}}{a_{x_{2}}-a_{y_{2}}}\right|\le\frac{N^{\epsilon}}{a_{x_{2}}-a_{y_{2}}}\le\frac{N^{\epsilon}}{\left(1-\frac{1}{C}\right)a_{x_{2}}}\ll\frac{N^{\epsilon}}{C^{N^{1/4}}},\end{align*}
we see that for sufficiently large N, the integer
![]() $n_{2}$
is uniquely determined by the values of
$n_{2}$
is uniquely determined by the values of
![]() $x_{1},x_{2},y_{1},y_{2},n_{1}$
. It is therefore sufficient to bound the number of possible values of
$x_{1},x_{2},y_{1},y_{2},n_{1}$
. It is therefore sufficient to bound the number of possible values of
![]() $y_{2}$
. There are
$y_{2}$
. There are
![]() $O\!\left(\log N\right)$
values of
$O\!\left(\log N\right)$
values of
![]() $y_{2}$
such that
$y_{2}$
such that
![]() $x_{2}-y_{2}\le5\log_{C}N$
. We will therefore count the number of possible values of
$x_{2}-y_{2}\le5\log_{C}N$
. We will therefore count the number of possible values of
![]() $y_{2}$
such that
$y_{2}$
such that
![]() $x_{2}-y_{2}>5\log_{C}N$
. For such
$x_{2}-y_{2}>5\log_{C}N$
. For such
![]() $y_{2}$
we have
$y_{2}$
we have
and therefore
 \begin{align*}n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right) & =n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)+O\!\left(N^{\epsilon}\right)=n_{2}a_{x_{2}}\!\left(1-\frac{a_{y_{2}}}{a_{x_{2}}}+O\!\left(\frac{N^{\epsilon}}{C^{N^{1/4}}}\right)\right)\\[5pt] & =n_{2}a_{x_{2}}\!\left(1+O\!\left(N^{-5}\right)\right)\!.\end{align*}
\begin{align*}n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right) & =n_{2}\!\left(a_{x_{2}}-a_{y_{2}}\right)+O\!\left(N^{\epsilon}\right)=n_{2}a_{x_{2}}\!\left(1-\frac{a_{y_{2}}}{a_{x_{2}}}+O\!\left(\frac{N^{\epsilon}}{C^{N^{1/4}}}\right)\right)\\[5pt] & =n_{2}a_{x_{2}}\!\left(1+O\!\left(N^{-5}\right)\right)\!.\end{align*}
Hence, given
![]() $\left(y_{2},n_{2}\right)$
and
$\left(y_{2},n_{2}\right)$
and
![]() $\left(y'_{\!\!2},n'_{\!\!2}\right)$
such that
$\left(y'_{\!\!2},n'_{\!\!2}\right)$
such that
![]() $x_{2}-y_{2}>5\log_{C}N$
and
$x_{2}-y_{2}>5\log_{C}N$
and
![]() $x_{2}-y'_{\!\!2}>5\log_{C}N$
, we have
$x_{2}-y'_{\!\!2}>5\log_{C}N$
, we have
and since
![]() $\left|n_{2}\right|\le N^{4}$
we conclude that
$\left|n_{2}\right|\le N^{4}$
we conclude that
so in fact
![]() $n'_{\!\!2}=n_{2}$
. We therefore see that the value of
$n'_{\!\!2}=n_{2}$
. We therefore see that the value of
![]() $n_{2}$
is identical for each
$n_{2}$
is identical for each
![]() $y_{2}$
such that
$y_{2}$
such that
![]() $x_{2}-y_{2}>5\log_{C}N$
. But, for such
$x_{2}-y_{2}>5\log_{C}N$
. But, for such
![]() $y_{2}$
, (2·2) gives
$y_{2}$
, (2·2) gives
 \begin{align*}a_{y_{2}}\in\left[a_{x_{2}}-\frac{n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)}{n_{2}}-\frac{N^{\epsilon}}{n_{2}},a_{x_{2}}-\frac{n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)}{n_{2}}+\frac{N^{\epsilon}}{n_{2}}\right]\end{align*}
\begin{align*}a_{y_{2}}\in\left[a_{x_{2}}-\frac{n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)}{n_{2}}-\frac{N^{\epsilon}}{n_{2}},a_{x_{2}}-\frac{n_{1}\!\left(a_{x_{1}}-a_{y_{1}}\right)}{n_{2}}+\frac{N^{\epsilon}}{n_{2}}\right]\end{align*}
so that
![]() $a_{y_{2}}$
lies in an interval of length
$a_{y_{2}}$
lies in an interval of length
![]() $O\!\left(N^{\epsilon}\right)$
, and since
$O\!\left(N^{\epsilon}\right)$
, and since
there could be at most
![]() $O\!\left(N^{\epsilon}\right)$
values of
$O\!\left(N^{\epsilon}\right)$
values of
![]() $y_{2}$
in this interval.
$y_{2}$
in this interval.
As an immediate corollary of Lemma 2·2 and Proposition 2·3, we obtain an upper bound for
![]() $V_{N}\!\left(L\right)$
.
$V_{N}\!\left(L\right)$
.
Corollary 2·4. Let
![]() $1\le L<N$
and let
$1\le L<N$
and let
![]() $\epsilon < 0$
We have
$\epsilon < 0$
We have
Proof. We use the bound
![]() $\widehat{\rho}\ll1$
and Lemma 2·2 to conclude that
$\widehat{\rho}\ll1$
and Lemma 2·2 to conclude that
 \begin{align*}V_{N}\!\left(L\right)\ll\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne\left|n_{1}\right|\le N^{4}\\ 1\le x_{1}\ne y_{1}\le N}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\sum_{\substack{0\ne\left|n_{2}\right|\le N^{4}\\ 1\le x_{2}\ne y_{2}\le N\\ \max\left\{ x_{1},x_{2},y_{1},y_{2}\right\} >N^{1/4}\\ \left|n_{1}\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\left(a_{x_{2}}-a_{y_{2}}\right)\right|\le N^{\epsilon/2}}}\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)+N^{-1}.\end{align*}
\begin{align*}V_{N}\!\left(L\right)\ll\frac{L^{2}}{N^{4}}\sum_{\substack{0\ne\left|n_{1}\right|\le N^{4}\\ 1\le x_{1}\ne y_{1}\le N}}\widehat{\Delta}\!\left(\frac{n_{1}L}{N}\right)\sum_{\substack{0\ne\left|n_{2}\right|\le N^{4}\\ 1\le x_{2}\ne y_{2}\le N\\ \max\left\{ x_{1},x_{2},y_{1},y_{2}\right\} >N^{1/4}\\ \left|n_{1}\left(a_{x_{1}}-a_{y_{1}}\right)-n_{2}\left(a_{x_{2}}-a_{y_{2}}\right)\right|\le N^{\epsilon/2}}}\widehat{\Delta}\!\left(\frac{n_{2}L}{N}\right)+N^{-1}.\end{align*}
By symmetry we can assume that
![]() $y_{1}<x_{1},$
$y_{1}<x_{1},$
![]() $x_{2}\le x_{1}$
and
$x_{2}\le x_{1}$
and
![]() $y_{2}<x_{2}$
, so that by the bound
$y_{2}<x_{2}$
, so that by the bound
![]() $\widehat{\Delta}\ll1$
and by Proposition 2·3, the inner summation is
$\widehat{\Delta}\ll1$
and by Proposition 2·3, the inner summation is
![]() $O\!\left(N^{\epsilon/2}\log N\right)$
. Hence, Lemma 2·1 gives the required bound (2·5).
$O\!\left(N^{\epsilon/2}\log N\right)$
. Hence, Lemma 2·1 gives the required bound (2·5).
3. Proofs of Theorems 1·1 and 1·2
We are now ready to prove Theorem 1·1.
Proof of Theorem 1·1. By (1·2) and (2·1) we have
Hence, for sufficiently large N we have

Denote by
![]() $ \chi_I $
the characteristic function of the interval I, and fix a smooth, compactly supported weight function
$ \chi_I $
the characteristic function of the interval I, and fix a smooth, compactly supported weight function
![]() $\rho\in C_{c}^{\infty}\left(\mathbb{R}\right)$
such that
$\rho\in C_{c}^{\infty}\left(\mathbb{R}\right)$
such that
![]() $\chi_{I}\!\left(x\right)\le\rho\!\left(x\right)$
for all
$\chi_{I}\!\left(x\right)\le\rho\!\left(x\right)$
for all
![]() $ x\in \mathbb{R} $
. By Chebyshev’s inequality we conclude that for sufficiently large N we have
$ x\in \mathbb{R} $
. By Chebyshev’s inequality we conclude that for sufficiently large N we have

where we used (2·5) with
![]() $\epsilon/2$
.
$\epsilon/2$
.
We now turn to the proof of Theorem 1·2, that is, we will show that (1·1) (or equivalently (1·4)) holds for almost all
![]() $\alpha\in\mathbb{R}$
. It sufficient to prove this for
$\alpha\in\mathbb{R}$
. It sufficient to prove this for
![]() $\alpha\in I$
where I is a bounded interval. We first show that almost sure convergence of the pair correlation holds along a subsequence.
$\alpha\in I$
where I is a bounded interval. We first show that almost sure convergence of the pair correlation holds along a subsequence.
Lemma 3·1.
Let I be a bounded interval, and let
![]() $\epsilon>0$
. Assume that
$\epsilon>0$
. Assume that
![]() $L=L\!\left(N\right)=O\!\left(N^{1/2-\epsilon}\right)$
as
$L=L\!\left(N\right)=O\!\left(N^{1/2-\epsilon}\right)$
as
![]() $N\to\infty$
. Let
$N\to\infty$
. Let
![]() $N_{m}=m^{2}$
, and denote
$N_{m}=m^{2}$
, and denote
![]() $L_{m}=L\!\left(N_{m}\right)$
. Then for almost all
$L_{m}=L\!\left(N_{m}\right)$
. Then for almost all
![]() $\alpha\in I$
, we have
$\alpha\in I$
, we have
as
![]() $m\to\infty$
.
$m\to\infty$
.
Proof. Applying (2·5) as in (3·1), for every
![]() $\delta>0$
and N sufficiently large we have
$\delta>0$
and N sufficiently large we have

so that
the asymptotic (3·2) thus holds for almost all
![]() $\alpha\in I$
by the Borel–Cantelli lemma.
$\alpha\in I$
by the Borel–Cantelli lemma.
We now have all that is needed to prove Theorem 1·2.
Proof of Theorem 1·2. It is sufficient to show that
as
![]() $N\to\infty$
for almost all
$N\to\infty$
for almost all
![]() $\alpha\in I$
. Let
$\alpha\in I$
. Let
![]() $N_{m}=m^{2}$
. For any N there exists m such that
$N_{m}=m^{2}$
. For any N there exists m such that
![]() $N_{m-1}\le N<N_{m}$
. Moreover,
$N_{m-1}\le N<N_{m}$
. Moreover,
![]() ${N_{m}}/{N}=1+O\!\left(m^{-1}\right)$
, and by the assumption
${N_{m}}/{N}=1+O\!\left(m^{-1}\right)$
, and by the assumption
we have
thus, there exists a constant
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $\delta>0$
, for sufficiently large N we have
$\delta>0$
, for sufficiently large N we have
 \begin{align*}R_{N}^{2}\!\left(L,\alpha,\Delta\right) & \le\frac{N_{m}}{N}R_{N_{m}}^{2}\!\left(L\cdot\frac{N_{m}}{N},\alpha,\Delta\right)\\[5pt] & \le\left(1+Cm^{-1}\right)R_{N_{m}}^{2}\!\left(\left(L_{m}+\delta\right)\cdot\left(1+Cm^{-1}\right)\!,\alpha,\Delta\right)\!;\end{align*}
\begin{align*}R_{N}^{2}\!\left(L,\alpha,\Delta\right) & \le\frac{N_{m}}{N}R_{N_{m}}^{2}\!\left(L\cdot\frac{N_{m}}{N},\alpha,\Delta\right)\\[5pt] & \le\left(1+Cm^{-1}\right)R_{N_{m}}^{2}\!\left(\left(L_{m}+\delta\right)\cdot\left(1+Cm^{-1}\right)\!,\alpha,\Delta\right)\!;\end{align*}
by applying Lemma 3·1 with
![]() $\left(L+\delta\right)\cdot\left(1+CN^{-1/2}\right)$
instead of L (and therefore with
$\left(L+\delta\right)\cdot\left(1+CN^{-1/2}\right)$
instead of L (and therefore with
![]() $\left(L_m+\delta\right)\cdot\left(1+Cm^{-1}\right)$
instead of
$\left(L_m+\delta\right)\cdot\left(1+Cm^{-1}\right)$
instead of
![]() $L_m$
), as
$L_m$
), as
![]() $m\to\infty$
we have
$m\to\infty$
we have
 \begin{align*}R_{N_{m}}^{2}\!\left(\left(L_{m}+\delta\right)\cdot\left(1+Cm^{-1}\right)\!,\alpha,\Delta\right) & =\left(L_{m}+\delta\right)\cdot\left(1+Cm^{-1}\right)+o\!\left(1\right)\\[5pt] & =L_{m}+\delta+o\!\left(1\right)\end{align*}
\begin{align*}R_{N_{m}}^{2}\!\left(\left(L_{m}+\delta\right)\cdot\left(1+Cm^{-1}\right)\!,\alpha,\Delta\right) & =\left(L_{m}+\delta\right)\cdot\left(1+Cm^{-1}\right)+o\!\left(1\right)\\[5pt] & =L_{m}+\delta+o\!\left(1\right)\end{align*}
for all
![]() $\alpha\in I_{\delta}$
, where
$\alpha\in I_{\delta}$
, where
![]() $I_{\delta}$
is a full measure set in I
$I_{\delta}$
is a full measure set in I
![]() $\big($
note that
$\big($
note that
![]() $L_{m}=o\!\left(m\right)$
by the assumption
$L_{m}=o\!\left(m\right)$
by the assumption
![]() $L=O\!\left(N^{1/2-\epsilon}\right)\!\big)$
. Hence, for sufficiently large N we have
$L=O\!\left(N^{1/2-\epsilon}\right)\!\big)$
. Hence, for sufficiently large N we have
for all
![]() $\alpha\in I_{\delta}$
. Symmetrically,
$\alpha\in I_{\delta}$
. Symmetrically,
for
![]() $\alpha$
in a full measure set in I (depending on
$\alpha$
in a full measure set in I (depending on
![]() $\delta$
); since
$\delta$
); since
![]() $\delta>0$
can be taken arbitrarily small along a countable sequence of values, and a countable intersection of full measure sets is still of full measure, the bounds (3·5) and (3·6) imply (3·4) for almost all
$\delta>0$
can be taken arbitrarily small along a countable sequence of values, and a countable intersection of full measure sets is still of full measure, the bounds (3·5) and (3·6) imply (3·4) for almost all
![]() $\alpha\in I$
.
$\alpha\in I$
.
Remark. The faster L grows, the sparser the subsequence
![]() $N_{m}$
one has to take in order to apply the Borel–Cantelli lemma in the proof of Lemma 3·1. On the other hand, since we require the condition
$N_{m}$
one has to take in order to apply the Borel–Cantelli lemma in the proof of Lemma 3·1. On the other hand, since we require the condition
![]() $L_{m}=o\!\left(m\right)\!,$
the subsequence
$L_{m}=o\!\left(m\right)\!,$
the subsequence
![]() $N_{m}$
cannot be too sparse. For example, if
$N_{m}$
cannot be too sparse. For example, if
![]() $L=N^{s},$
and
$L=N^{s},$
and
![]() $N_{m}=\lfloor m^{t}\rfloor$
, one needs
$N_{m}=\lfloor m^{t}\rfloor$
, one needs
![]() $t>{1}/({1-s})$
for (3·3) to hold, but also
$t>{1}/({1-s})$
for (3·3) to hold, but also
![]() $t<{1}/{s}$
, so that
$t<{1}/{s}$
, so that
![]() $s<1/2$
. This explains why the above argument only works for L growing slower than
$s<1/2$
. This explains why the above argument only works for L growing slower than
![]() $N^{1/2}.$
$N^{1/2}.$
4. Higher order correlations – proof of Theorem 1·3
Taking expectations w.r.t x, for all
![]() $k\ge2$
, we have
$k\ge2$
, we have
 \begin{align}\mathbb{E}\left[\left(S_{N}\!\left(L,\alpha\right)\right)^{k}\right] & =\sum_{j_{1},\dots,j_{k}=1}^{N}\sum_{n_{1},\dots,n_{k}\in\mathbb{Z}}\int_{0}^{1}\prod_{i=1}^{k}\chi\!\left(\frac{\alpha a_{j_{i}}-x+n_{i}}{L/N}\right)\,dx\\[5pt] & =\sum_{j_{1},\dots,j_{k}=1}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\int_{\mathbb{R}}\prod_{i=1}^{k-1}\chi\!\left(\frac{\alpha a_{j_{i}}-x+n_{i}}{L/N}\right)\chi\!\left(\frac{\alpha a_{j_{k}}-x}{L/N}\right)\,dx\nonumber \\[5pt] & =\frac{L}{N}\sum_{j_{1},\dots,j_{k}=1}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\Delta\!\left(\frac{\alpha a_{j_{1}}-\alpha a_{j_{k}}+n_{1}}{L/N},\dots,\frac{\alpha a_{j_{k-1}}-\alpha a_{j_{k}}+n_{k-1}}{L/N}\!\right)\!,\nonumber \end{align}
\begin{align}\mathbb{E}\left[\left(S_{N}\!\left(L,\alpha\right)\right)^{k}\right] & =\sum_{j_{1},\dots,j_{k}=1}^{N}\sum_{n_{1},\dots,n_{k}\in\mathbb{Z}}\int_{0}^{1}\prod_{i=1}^{k}\chi\!\left(\frac{\alpha a_{j_{i}}-x+n_{i}}{L/N}\right)\,dx\\[5pt] & =\sum_{j_{1},\dots,j_{k}=1}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\int_{\mathbb{R}}\prod_{i=1}^{k-1}\chi\!\left(\frac{\alpha a_{j_{i}}-x+n_{i}}{L/N}\right)\chi\!\left(\frac{\alpha a_{j_{k}}-x}{L/N}\right)\,dx\nonumber \\[5pt] & =\frac{L}{N}\sum_{j_{1},\dots,j_{k}=1}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\Delta\!\left(\frac{\alpha a_{j_{1}}-\alpha a_{j_{k}}+n_{1}}{L/N},\dots,\frac{\alpha a_{j_{k-1}}-\alpha a_{j_{k}}+n_{k-1}}{L/N}\!\right)\!,\nonumber \end{align}
where

we have (see [ Reference Hauke and Zafeiropoulos3 , lemma 13])
For
![]() $0\le j\le k,$
denote by
$0\le j\le k,$
denote by
![]() $\begin{Bmatrix}k\\[5pt] j\end{Bmatrix}$
the Stirling number of the second kind, i.e., the number of ways to partition a set of k elements into j non-empty subsets. We partition the sum over
$\begin{Bmatrix}k\\[5pt] j\end{Bmatrix}$
the Stirling number of the second kind, i.e., the number of ways to partition a set of k elements into j non-empty subsets. We partition the sum over
![]() $j_{1},\dots,j_{k}$
on the right-hand side of (4·1) into sums with j distinct indices. The term corresponding to
$j_{1},\dots,j_{k}$
on the right-hand side of (4·1) into sums with j distinct indices. The term corresponding to
![]() $j=1$
is clearly equal to L. Recalling the definition (1·5) of the j-level correlation functions
$j=1$
is clearly equal to L. Recalling the definition (1·5) of the j-level correlation functions
![]() $R_{N}^{j}\left(L,\alpha,\Delta\right)$
, we then have
$R_{N}^{j}\left(L,\alpha,\Delta\right)$
, we then have
 \begin{align*}\mathbb{E}\left[\left(S_{N}\!\left(L,\alpha\right)\right)^{k}\right]=L+L\sum_{j=2}^{k}\begin{Bmatrix}k\\[5pt] j\end{Bmatrix}R_{N}^{j}\left(L,\alpha,\Delta\right)\!.\end{align*}
\begin{align*}\mathbb{E}\left[\left(S_{N}\!\left(L,\alpha\right)\right)^{k}\right]=L+L\sum_{j=2}^{k}\begin{Bmatrix}k\\[5pt] j\end{Bmatrix}R_{N}^{j}\left(L,\alpha,\Delta\right)\!.\end{align*}
In view of Lemma A·1, Theorem 1·3 will be a direct consequence of the following proposition.
Proposition 4·1.
Let
![]() $L=L\!\left(N\right)$
such that for all
$L=L\!\left(N\right)$
such that for all
![]() $\eta>0$
we have
$\eta>0$
we have
![]() $L=O\!\left(N^{\eta}\right)$
, and assume that there exists
$L=O\!\left(N^{\eta}\right)$
, and assume that there exists
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
![]() $L\!\left(N+1\right)-L\!\left(N\right)=O\!\left(N^{-\epsilon}\right)$
. Then for almost all
$L\!\left(N+1\right)-L\!\left(N\right)=O\!\left(N^{-\epsilon}\right)$
. Then for almost all
![]() $\alpha\in\mathbb{R}$
, we have
$\alpha\in\mathbb{R}$
, we have
for all
![]() $j\ge2$
and all
$j\ge2$
and all
![]() $s>0$
.
$s>0$
.
We apply the following strategy for proving Proposition 4·1. We first prove an analogous result with a smooth test function along a subsequence. We then unsmooth along the subsequence, and finally deduce the result along the full sequence. We would like to use the results of [
Reference Chaubey and Yesha2
], and for that it would be more convenient to work with a “transformed” correlation function: for
![]() $k\ge2$
and for a smooth, compactly supported function
$k\ge2$
and for a smooth, compactly supported function
![]() $\psi\;:\;\mathbb{R}^{k-1}\to\mathbb{R}$
(which may depend on N), we denote the smoothed k-level correlation function
$\psi\;:\;\mathbb{R}^{k-1}\to\mathbb{R}$
(which may depend on N), we denote the smoothed k-level correlation function
 \begin{align*}R_{N}^{k}\!\left(L,\alpha,\psi\right)=\frac{1}{N}\sum_{\substack{j_{1},\dots,j_{k}=1\\ \mathrm{distinct}}}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\psi\!\left(\frac{\alpha a_{j_{1}}-\alpha a_{j_{k}}+n_{1}}{L/N},\dots,\frac{\alpha a_{j_{k-1}}-\alpha a_{j_{k}}+n_{k-1}}{L/N}\right)\end{align*}
\begin{align*}R_{N}^{k}\!\left(L,\alpha,\psi\right)=\frac{1}{N}\sum_{\substack{j_{1},\dots,j_{k}=1\\ \mathrm{distinct}}}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\psi\!\left(\frac{\alpha a_{j_{1}}-\alpha a_{j_{k}}+n_{1}}{L/N},\dots,\frac{\alpha a_{j_{k-1}}-\alpha a_{j_{k}}+n_{k-1}}{L/N}\right)\end{align*}
and the transformed smoothed k-level correlation function
 \begin{align*}\tilde{R}_{N}^{k}\!\left(\alpha,\psi\right)=\frac{1}{N}\sum_{\substack{j_{1},\dots,j_{k}=1\\ \mathrm{distinct}}}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\psi\!\left(N\left(\alpha a_{j_{1}}-\alpha a_{j_{2}}+n_{1}\right)\!,\dots,N\left(\alpha a_{j_{k-1}}-\alpha a_{j_{k}}+n_{k-1}\right)\right)\!.\end{align*}
\begin{align*}\tilde{R}_{N}^{k}\!\left(\alpha,\psi\right)=\frac{1}{N}\sum_{\substack{j_{1},\dots,j_{k}=1\\ \mathrm{distinct}}}^{N}\sum_{n_{1},\dots,n_{k-1}\in\mathbb{Z}}\psi\!\left(N\left(\alpha a_{j_{1}}-\alpha a_{j_{2}}+n_{1}\right)\!,\dots,N\left(\alpha a_{j_{k-1}}-\alpha a_{j_{k}}+n_{k-1}\right)\right)\!.\end{align*}
Then
where
For the transformed correlation function we have the following
![]() $L^{2}-$
norm estimate: let I be a bounded interval, and let
$L^{2}-$
norm estimate: let I be a bounded interval, and let
where
Lemma 4·2.
Let
![]() $k\ge2$
. For each
$k\ge2$
. For each
![]() $\eta>0$
there exists
$\eta>0$
there exists
![]() $r=r\left(\eta\right)$
such that
$r=r\left(\eta\right)$
such that
where
![]() $\left\Vert \psi\right\Vert _{r,1}=\sum\limits _{\left|\alpha\right|\le r}\left\Vert \partial^{\alpha}\psi\right\Vert _{1}$
.
$\left\Vert \psi\right\Vert _{r,1}=\sum\limits _{\left|\alpha\right|\le r}\left\Vert \partial^{\alpha}\psi\right\Vert _{1}$
.
Proof. For a smooth, compactly supported, non-negative weight function
![]() $\rho\in C_{c}^{\infty}\left(\mathbb{R}\right)\!,\,\rho\ge0$
, denote
$\rho\in C_{c}^{\infty}\left(\mathbb{R}\right)\!,\,\rho\ge0$
, denote
Then proposition 7 in [
Reference Chaubey and Yesha2
] implies that for each
![]() $\eta>0$
there exists
$\eta>0$
there exists
![]() $r=r\left(\eta\right)$
such that
$r=r\left(\eta\right)$
such that
while the term
![]() $\left\Vert \psi\right\Vert _{r,1}^{2}$
is not explicitly stated there, it follows from the proof, which we now sketch (for the full details we refer the reader to [
Reference Chaubey and Yesha2
]): for
$\left\Vert \psi\right\Vert _{r,1}^{2}$
is not explicitly stated there, it follows from the proof, which we now sketch (for the full details we refer the reader to [
Reference Chaubey and Yesha2
]): for
![]() $x=\left(x_{1},\dots,x_{k}\right)\!,$
denote
$x=\left(x_{1},\dots,x_{k}\right)\!,$
denote
by the Poisson summation formula, we have
 \begin{align*}\tilde{R}_{N}^{k}\!\left(\alpha,\psi\right)=C_{k}\!\left(N\right)\widehat{\psi}\left(0\right)+\frac{1}{N^{k}}\sum_{0\ne n\in\mathbb{Z}^{k-1}}\widehat{\psi}\left(\frac{n}{N}\right)\sum_{\substack{x=\left(x_{1},\dots,x_{k}\right)\\ 1\le x_{1},\dots,x_{k}\le N\,\mathrm{distinct}}}e\left(\alpha n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)\right)\!,\end{align*}
\begin{align*}\tilde{R}_{N}^{k}\!\left(\alpha,\psi\right)=C_{k}\!\left(N\right)\widehat{\psi}\left(0\right)+\frac{1}{N^{k}}\sum_{0\ne n\in\mathbb{Z}^{k-1}}\widehat{\psi}\left(\frac{n}{N}\right)\sum_{\substack{x=\left(x_{1},\dots,x_{k}\right)\\ 1\le x_{1},\dots,x_{k}\le N\,\mathrm{distinct}}}e\left(\alpha n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)\right)\!,\end{align*}
and hence
 \begin{align*}V\!\left(\tilde{R}_{N}^{k}\!\left(\psi\right)\!,\rho\right)=\frac{1}{N^{2k}}\sum_{0\ne n,m\in\mathbb{Z}^{k-1}}\widehat{\psi}\left(\frac{n}{N}\right)\overline{\widehat{\psi}\left(\frac{m}{N}\right)}\sum^{*}\widehat{\rho}\left(n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)-m\cdot\Delta_{\left(a_{n}\right)}\left(y\right)\right)\!,\end{align*}
\begin{align*}V\!\left(\tilde{R}_{N}^{k}\!\left(\psi\right)\!,\rho\right)=\frac{1}{N^{2k}}\sum_{0\ne n,m\in\mathbb{Z}^{k-1}}\widehat{\psi}\left(\frac{n}{N}\right)\overline{\widehat{\psi}\left(\frac{m}{N}\right)}\sum^{*}\widehat{\rho}\left(n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)-m\cdot\Delta_{\left(a_{n}\right)}\left(y\right)\right)\!,\end{align*}
where the range of the summation
![]() $\sum\limits ^{*}$
is over
$\sum\limits ^{*}$
is over
![]() $x=\left(x_{1},\dots,x_{k}\right)$
where
$x=\left(x_{1},\dots,x_{k}\right)$
where
![]() $1\le x_{1},\dots,x_{k}\le N$
are distinct, and
$1\le x_{1},\dots,x_{k}\le N$
are distinct, and
![]() $y=\left(y_{1},\dots,y_{k}\right)$
where
$y=\left(y_{1},\dots,y_{k}\right)$
where
![]() $1\le y_{1},\dots,y_{k}\le N$
are distinct. Fix
$1\le y_{1},\dots,y_{k}\le N$
are distinct. Fix
![]() $\epsilon>0$
; by splitting the summation over n, m into different ranges and using the bounds
$\epsilon>0$
; by splitting the summation over n, m into different ranges and using the bounds
![]() $\widehat{\rho}\ll1$
,
$\widehat{\rho}\ll1$
,
![]() $\left|\widehat{\psi}\right|\le\left\Vert \psi\right\Vert _{1}\le\left\Vert \psi\right\Vert _{r,1}$
and
$\left|\widehat{\psi}\right|\le\left\Vert \psi\right\Vert _{1}\le\left\Vert \psi\right\Vert _{r,1}$
and
![]() $\left|\widehat{\psi}\right|\ll\left\Vert \psi\right\Vert _{r,1}\left\Vert x\right\Vert _{\infty}^{-r}$
(for arbitrarily large r), we obtain
$\left|\widehat{\psi}\right|\ll\left\Vert \psi\right\Vert _{r,1}\left\Vert x\right\Vert _{\infty}^{-r}$
(for arbitrarily large r), we obtain
 \begin{align*}V\!\left(\tilde{R}_{N}^{k}\!\left(\psi\right)\!,\rho\right) & \ll\left\Vert \psi\right\Vert _{r,1}^{2}\Bigl(\frac{1}{N^{2k}}\sum_{\left\Vert n\right\Vert _{\infty},\left\Vert m\right\Vert _{\infty}>N^{1+\epsilon}}\left\Vert \frac{n}{N}\right\Vert _{\infty}^{-r}\left\Vert \frac{m}{N}\right\Vert _{\infty}^{-r}\sum^{*}1\\[5pt] & \quad +\frac{1}{N^{2k}}\sum_{\left\Vert n\right\Vert _{\infty}>N^{1+\epsilon},0<\left\Vert m\right\Vert _{\infty}\le N^{1+\epsilon}}\left\Vert \frac{n}{N}\right\Vert _{\infty}^{-r}\sum^{*}1\\[5pt] & \quad +\frac{1}{N^{2k}}\sum_{0<\left\Vert n\right\Vert _{\infty},\left\Vert m\right\Vert _{\infty}\le N^{1+\epsilon}}\sum^{*}\left|\widehat{\rho}\left(n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)-m\cdot\Delta_{\left(a_{n}\right)}\left(y\right)\right)\right|\Bigr).\end{align*}
\begin{align*}V\!\left(\tilde{R}_{N}^{k}\!\left(\psi\right)\!,\rho\right) & \ll\left\Vert \psi\right\Vert _{r,1}^{2}\Bigl(\frac{1}{N^{2k}}\sum_{\left\Vert n\right\Vert _{\infty},\left\Vert m\right\Vert _{\infty}>N^{1+\epsilon}}\left\Vert \frac{n}{N}\right\Vert _{\infty}^{-r}\left\Vert \frac{m}{N}\right\Vert _{\infty}^{-r}\sum^{*}1\\[5pt] & \quad +\frac{1}{N^{2k}}\sum_{\left\Vert n\right\Vert _{\infty}>N^{1+\epsilon},0<\left\Vert m\right\Vert _{\infty}\le N^{1+\epsilon}}\left\Vert \frac{n}{N}\right\Vert _{\infty}^{-r}\sum^{*}1\\[5pt] & \quad +\frac{1}{N^{2k}}\sum_{0<\left\Vert n\right\Vert _{\infty},\left\Vert m\right\Vert _{\infty}\le N^{1+\epsilon}}\sum^{*}\left|\widehat{\rho}\left(n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)-m\cdot\Delta_{\left(a_{n}\right)}\left(y\right)\right)\right|\Bigr).\end{align*}
The contribution of the first two terms is negligible by a trivial estimate, and so is the contribution of the third term restricted to the range
![]() $\left|n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)-m\cdot\Delta_{\left(a_{n}\right)}\left(y\right)\right|>N^{\epsilon}$
(choosing r sufficiently large depending on
$\left|n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)-m\cdot\Delta_{\left(a_{n}\right)}\left(y\right)\right|>N^{\epsilon}$
(choosing r sufficiently large depending on
![]() $\epsilon$
). The rest of the contribution from the third term is then bounded by [
Reference Chaubey and Yesha2
, proposition 2] which states that there are at most
$\epsilon$
). The rest of the contribution from the third term is then bounded by [
Reference Chaubey and Yesha2
, proposition 2] which states that there are at most
![]() $O\!\left(N^{2k-1+4k\epsilon}\right)$
values of n, m, x, y in the above ranges such that
$O\!\left(N^{2k-1+4k\epsilon}\right)$
values of n, m, x, y in the above ranges such that
![]() $\left|n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)-m\cdot\Delta_{\left(a_{n}\right)}\left(y\right)\right|\le N^{\epsilon}$
, which gives (4·6).
$\left|n\cdot\Delta_{\left(a_{n}\right)}\left(x\right)-m\cdot\Delta_{\left(a_{n}\right)}\left(y\right)\right|\le N^{\epsilon}$
, which gives (4·6).
Finally, if we choose
![]() $\rho$
such that
$\rho$
such that
![]() $\rho\ge \chi_{I}$
, then
$\rho\ge \chi_{I}$
, then
and (4·5) follows.
Fix
![]() $\eta>0$
, and let
$\eta>0$
, and let
![]() $r=r\left(\eta\right)>1$
be as in Lemma 4·2; let
$r=r\left(\eta\right)>1$
be as in Lemma 4·2; let
![]() $0<\epsilon<1$
,
$0<\epsilon<1$
,
![]() $\delta=N^{-\frac{\epsilon}{8r}}$
, and assume that
$\delta=N^{-\frac{\epsilon}{8r}}$
, and assume that
![]() $\psi\in C_{c}^{\infty}\left(\mathbb{R}^{k-1}\right)$
is a smooth approximation to
$\psi\in C_{c}^{\infty}\left(\mathbb{R}^{k-1}\right)$
is a smooth approximation to
![]() $\Delta$
, such that
$\Delta$
, such that
![]() $\left\Vert \Delta-\psi\right\Vert _{\infty}\ll\delta$
and such that
$\left\Vert \Delta-\psi\right\Vert _{\infty}\ll\delta$
and such that
![]() $\left\Vert \psi\right\Vert _{r,1}\ll\delta^{-r}$
. By (4·2), if L grows slower than any power of N, then
$\left\Vert \psi\right\Vert _{r,1}\ll\delta^{-r}$
. By (4·2), if L grows slower than any power of N, then
Moreover, we have
We deduce almost sure convergence along a subsequence.
Lemma 4·3.
Let
![]() $L=L\!\left(N\right)$
be such that for all
$L=L\!\left(N\right)$
be such that for all
![]() $\eta>0$
we have
$\eta>0$
we have
![]() $L=O\!\left(N^{\eta}\right)$
and let
$L=O\!\left(N^{\eta}\right)$
and let
![]() $k\ge2$
. Let
$k\ge2$
. Let
![]() $0<\epsilon<1$
,
$0<\epsilon<1$
,
![]() $N_{m}=\lfloor m^{1+\epsilon}\rfloor$
, and denote
$N_{m}=\lfloor m^{1+\epsilon}\rfloor$
, and denote
![]() $L_{m}=L\!\left(N_{m}\right)$
. Then for almost all
$L_{m}=L\!\left(N_{m}\right)$
. Then for almost all
![]() $\alpha\in I$
, we have
$\alpha\in I$
, we have
for all
![]() $s>0,$
as
$s>0,$
as
![]() $m\to\infty$
,
$m\to\infty$
,
Proof. It is sufficient to show that for any fixed
![]() $s>0$
, (4·7) holds for almost all
$s>0$
, (4·7) holds for almost all
![]() $\alpha\in I$
. By identity (4·4), Lemma 4·2, and the upper bound on L, for each
$\alpha\in I$
. By identity (4·4), Lemma 4·2, and the upper bound on L, for each
![]() $\eta>0$
there exists
$\eta>0$
there exists
![]() $r=r\left(\eta\right)$
such that
$r=r\left(\eta\right)$
such that
 \begin{gather*}\int_{I}\!\left(L_{m}^{s}\!\left(R_{N_{m}}^{k}\!\left(L_{m},\alpha,\psi\right)-C_{k}\!\left(N_{m}\right)\widehat{\tilde{\psi}_{L_{m}}}\left(0\right)\right)\right)^{2}\,d\alpha=L_{m}^{2s}V\!\left(\tilde{R}_{N_{m}}^{k}\left(\tilde{\psi}_{L_{m}}\right)\right)\\[5pt] =O\!\left(\left\Vert \tilde{\psi}_{L_{m}}\right\Vert _{r,1}^{2}L_{m}^{2s}N_{m}^{-1+\eta}\right)=O\!\left(N_{m}^{-1+\frac{\epsilon}{4}+3\eta}\right)=O\!\left(m^{\left(1+\epsilon\right)\left(-1+\frac{\epsilon}{4}+3\eta\right)}\right)\!.\end{gather*}
\begin{gather*}\int_{I}\!\left(L_{m}^{s}\!\left(R_{N_{m}}^{k}\!\left(L_{m},\alpha,\psi\right)-C_{k}\!\left(N_{m}\right)\widehat{\tilde{\psi}_{L_{m}}}\left(0\right)\right)\right)^{2}\,d\alpha=L_{m}^{2s}V\!\left(\tilde{R}_{N_{m}}^{k}\left(\tilde{\psi}_{L_{m}}\right)\right)\\[5pt] =O\!\left(\left\Vert \tilde{\psi}_{L_{m}}\right\Vert _{r,1}^{2}L_{m}^{2s}N_{m}^{-1+\eta}\right)=O\!\left(N_{m}^{-1+\frac{\epsilon}{4}+3\eta}\right)=O\!\left(m^{\left(1+\epsilon\right)\left(-1+\frac{\epsilon}{4}+3\eta\right)}\right)\!.\end{gather*}
Hence, by the Borel–Cantelli lemma, for
![]() $\eta$
sufficiently small we have
$\eta$
sufficiently small we have
for almost all
![]() $\alpha\in I$
, and in particular
$\alpha\in I$
, and in particular
where we used again the upper bound on L.
Let
![]() $\psi=\psi_{\pm}$
be approximations to
$\psi=\psi_{\pm}$
be approximations to
![]() $\Delta$
satisfying the above assumptions such that
$\Delta$
satisfying the above assumptions such that
![]() $\psi_{-}\le\Delta\le\psi_{+}$
; a simple way to construct such approximations is to convolve the functions
$\psi_{-}\le\Delta\le\psi_{+}$
; a simple way to construct such approximations is to convolve the functions
with
![]() $\varphi_{\delta/10}\left(t\right)$
, where
$\varphi_{\delta/10}\left(t\right)$
, where
![]() $\varphi_{\varepsilon}\left(t\right)=\varepsilon^{-\left(k-1\right)}\varphi\left(t/\varepsilon\right)$
, and
$\varphi_{\varepsilon}\left(t\right)=\varepsilon^{-\left(k-1\right)}\varphi\left(t/\varepsilon\right)$
, and
![]() $\varphi\in C_{c}^{\infty}\left(\mathbb{R}^{k-1}\right)$
is the standard mollifier. We then have
$\varphi\in C_{c}^{\infty}\left(\mathbb{R}^{k-1}\right)$
is the standard mollifier. We then have
substituting the asymptotics (4·8), we conclude that (4·7) holds for almost all
![]() $\alpha\in I$
.
$\alpha\in I$
.
We are now ready to prove Proposition 4·1.
Proof of Proposition
4·1. The argument is similar to that of the proof of Theorem 1·2. Let
![]() $k\ge2$
; it is enough to show that for almost all
$k\ge2$
; it is enough to show that for almost all
![]() $\alpha\in I$
, we have
$\alpha\in I$
, we have
for all
![]() $s>0$
. Let
$s>0$
. Let
![]() $N_{m}=\lfloor m^{1+\epsilon/2}\rfloor$
, so that for any N there exists m such that
$N_{m}=\lfloor m^{1+\epsilon/2}\rfloor$
, so that for any N there exists m such that
![]() $N_{m-1}\le N<N_{m}$
. Moreover,
$N_{m-1}\le N<N_{m}$
. Moreover,
![]() ${N_{m}}/{N}=1+O\!\left(m^{-1}\right)$
, and by the assumption
${N_{m}}/{N}=1+O\!\left(m^{-1}\right)$
, and by the assumption
we have
hence, there exists a constant
![]() $C>0$
such that for sufficiently large N we have
$C>0$
such that for sufficiently large N we have
 \begin{align*}R_{N}^{k}\!\left(L,\alpha,\Delta\right) & \le\frac{N_{m}}{N}R_{N_{m}}^{k}\!\left(L\cdot\frac{N_{m}}{N},\alpha,\Delta\right)\\[5pt] & \le\left(1+Cm^{-1}\right)R_{N_{m}}^{k}\!\left(\left(L_{m}+CN_{m}^{-\epsilon/2}\right)\cdot\left(1+CN_{m}^{-\frac{1}{1+\epsilon/2}}\right)\!,\alpha,\Delta\right)\!;\end{align*}
\begin{align*}R_{N}^{k}\!\left(L,\alpha,\Delta\right) & \le\frac{N_{m}}{N}R_{N_{m}}^{k}\!\left(L\cdot\frac{N_{m}}{N},\alpha,\Delta\right)\\[5pt] & \le\left(1+Cm^{-1}\right)R_{N_{m}}^{k}\!\left(\left(L_{m}+CN_{m}^{-\epsilon/2}\right)\cdot\left(1+CN_{m}^{-\frac{1}{1+\epsilon/2}}\right)\!,\alpha,\Delta\right)\!;\end{align*}
by the upper bound on L and Lemma 4·3 with
![]() $\left(L+CN^{-\epsilon/2}\right)\cdot\left(1+CN^{-\frac{1}{1+\epsilon/2}}\right)$
instead of L, for almost all
$\left(L+CN^{-\epsilon/2}\right)\cdot\left(1+CN^{-\frac{1}{1+\epsilon/2}}\right)$
instead of L, for almost all
![]() $\alpha\in I$
we have
$\alpha\in I$
we have
 \begin{gather*}R_{N_{m}}^{k}\!\left(\left(L_{m}+CN_{m}^{-\epsilon/2}\right)\cdot\left(1+CN_{m}^{-\frac{1}{1+\epsilon/2}}\right)\!,\alpha,\Delta\right)\\[5pt] =\left(L_{m}+CN_{m}^{-\epsilon/2}\right)^{k-1}\cdot\left(1+CN_{m}^{-\frac{1}{1+\epsilon/2}}\right)^{k-1}+O\!\left(L_{m}^{-s}\right)=L_{m}^{k-1}+O\!\left(L_{m}^{-s}\right)\end{gather*}
\begin{gather*}R_{N_{m}}^{k}\!\left(\left(L_{m}+CN_{m}^{-\epsilon/2}\right)\cdot\left(1+CN_{m}^{-\frac{1}{1+\epsilon/2}}\right)\!,\alpha,\Delta\right)\\[5pt] =\left(L_{m}+CN_{m}^{-\epsilon/2}\right)^{k-1}\cdot\left(1+CN_{m}^{-\frac{1}{1+\epsilon/2}}\right)^{k-1}+O\!\left(L_{m}^{-s}\right)=L_{m}^{k-1}+O\!\left(L_{m}^{-s}\right)\end{gather*}
for all
![]() $s>0$
. Thus, for sufficiently large N we have (using again the upper bound on L), for almost all
$s>0$
. Thus, for sufficiently large N we have (using again the upper bound on L), for almost all
![]() $\alpha\in I$
we have
$\alpha\in I$
we have
for all
![]() $s>0$
. Similarly, for almost all
$s>0$
. Similarly, for almost all
![]() $\alpha\in I$
we have
$\alpha\in I$
we have
Acknowledgments
We thank Jens Marklof and Zeév Rudnick for stimulating discussions and for their comments.
Appendix A. Normal approximation to the Poisson distribution
We require a normal approximation to a random variable whose moments are close to the Poisson moments. Denote
 \begin{align*}\mu_{k}^{Poisson}\left(L\right)=\sum\limits _{j=0}^{k}\begin{Bmatrix}k\\[5pt] j\end{Bmatrix}L^{j}\end{align*}
\begin{align*}\mu_{k}^{Poisson}\left(L\right)=\sum\limits _{j=0}^{k}\begin{Bmatrix}k\\[5pt] j\end{Bmatrix}L^{j}\end{align*}
the kth moment of a Poisson-distributed random variable with parameter L, and
 \begin{align*}\mu_{k}^{normal}=\begin{cases}0 & k\,\text{odd}\\[5pt] \left(k-1\right)!! & k\,\text{even}\end{cases}\end{align*}
\begin{align*}\mu_{k}^{normal}=\begin{cases}0 & k\,\text{odd}\\[5pt] \left(k-1\right)!! & k\,\text{even}\end{cases}\end{align*}
the kth moment of a standard Gaussian random variable.
Lemma A·1.
Let
![]() $L=L\!\left(N\right)\to\infty$
as
$L=L\!\left(N\right)\to\infty$
as
![]() $N\to\infty$
, and let
$N\to\infty$
, and let
![]() $\left(X_{N}\right)_{N=1}^{\infty}$
be a sequence of random variables such that for all
$\left(X_{N}\right)_{N=1}^{\infty}$
be a sequence of random variables such that for all
![]() $j\ge1$
and for all
$j\ge1$
and for all
![]() $s>0$
we have
$s>0$
we have
as
![]() $N\to\infty$
. Then
$N\to\infty$
. Then
as
![]() $N\to\infty$
, where
$N\to\infty$
, where
![]() $\mathcal{N}\!\left(0,1\right)$
is the standard Gaussian distribution.
$\mathcal{N}\!\left(0,1\right)$
is the standard Gaussian distribution.
Proof. Let
![]() $\widehat{X_{N}}=({X_{N}-L})/{\sqrt{L}}.$
It is sufficient to prove that for all
$\widehat{X_{N}}=({X_{N}-L})/{\sqrt{L}}.$
It is sufficient to prove that for all
![]() $k\ge1$
we have
$k\ge1$
we have
![]() $\lim\limits _{N\to\infty}\mathbb{E}\left[\widehat{X_{N}}^{k}\right]=\mu_{k}^{normal}$
. By (A·1), we have
$\lim\limits _{N\to\infty}\mathbb{E}\left[\widehat{X_{N}}^{k}\right]=\mu_{k}^{normal}$
. By (A·1), we have
 \begin{align*}\mathbb{E}\left[\widehat{X_{N}}^{k}\right]=L^{-k/2}\sum_{j=0}^{k}\left(\begin{array}{c}{k}\\[2pt] {j}\end{array}\right)\left(\mu_{j}^{Poisson}\left(L\right)\right)^{j}\left(-L\right)^{k-j}+o\!\left(1\right)\!,\end{align*}
\begin{align*}\mathbb{E}\left[\widehat{X_{N}}^{k}\right]=L^{-k/2}\sum_{j=0}^{k}\left(\begin{array}{c}{k}\\[2pt] {j}\end{array}\right)\left(\mu_{j}^{Poisson}\left(L\right)\right)^{j}\left(-L\right)^{k-j}+o\!\left(1\right)\!,\end{align*}
so we have to show that for all
![]() $k\ge1$
we have
$k\ge1$
we have
 \begin{equation}L^{-k/2}\sum_{j=0}^{k}\left(\begin{array}{c}{k}\\[2pt] {j}\end{array}\right)\left(\mu_{j}^{Poisson}\left(L\right)\right)^{j}\left(-L\right)^{k-j}=\mu_{k}^{normal}+o\left(1\right)\!.\end{equation}
\begin{equation}L^{-k/2}\sum_{j=0}^{k}\left(\begin{array}{c}{k}\\[2pt] {j}\end{array}\right)\left(\mu_{j}^{Poisson}\left(L\right)\right)^{j}\left(-L\right)^{k-j}=\mu_{k}^{normal}+o\left(1\right)\!.\end{equation}
Let
![]() $Y_{L}$
be a Poisson-distributed random variable with parameter L and
$Y_{L}$
be a Poisson-distributed random variable with parameter L and
![]() $\widehat{Y_{L}}=({Y_{L}-L})/{\sqrt{L}}$
; we have to show that for all
$\widehat{Y_{L}}=({Y_{L}-L})/{\sqrt{L}}$
; we have to show that for all
![]() $k\ge1$
we have
$k\ge1$
we have
![]() $\lim\limits _{N\to\infty}\mathbb{E}\left[\widehat{Y_{L}}^{k}\right]=\mu_{k}^{normal}$
. Let
$\lim\limits _{N\to\infty}\mathbb{E}\left[\widehat{Y_{L}}^{k}\right]=\mu_{k}^{normal}$
. Let
![]() $M_{\widehat{Y_{L}}}\left(t\right)$
be the moment-generating function of
$M_{\widehat{Y_{L}}}\left(t\right)$
be the moment-generating function of
![]() $\widehat{Y_{L}}$
. Then for any t we have
$\widehat{Y_{L}}$
. Then for any t we have
 \begin{align}M_{\widehat{Y_{L}}}\left(t\right) & =e^{-t\sqrt{L}+L\left(e^{t/\sqrt{L}}-1\right)}=e^{-t\sqrt{L}+L\left(t/\sqrt{L}+t^{2}/\left(2L\right)+O\!\left(L^{-3/2}\right)\right)}\nonumber \\[5pt] & =e^{\frac{t^{2}}{2}+O(L^{-1/2})}\underset{N\to\infty}{\longrightarrow}e^{t^{2}/2}\end{align}
\begin{align}M_{\widehat{Y_{L}}}\left(t\right) & =e^{-t\sqrt{L}+L\left(e^{t/\sqrt{L}}-1\right)}=e^{-t\sqrt{L}+L\left(t/\sqrt{L}+t^{2}/\left(2L\right)+O\!\left(L^{-3/2}\right)\right)}\nonumber \\[5pt] & =e^{\frac{t^{2}}{2}+O(L^{-1/2})}\underset{N\to\infty}{\longrightarrow}e^{t^{2}/2}\end{align}
so that the limit is the moment-generating function of a standard Gaussian random variable. Since the convergence in (A·3) is uniform in a complex neighbourhood of
![]() $t=0$
and all the functions involved are (complex) analytic, convergence of the moments (which can be expressed as the derivatives of the moment-generating function evaluated at zero) easily follows from Cauchy’s integral formula.
$t=0$
and all the functions involved are (complex) analytic, convergence of the moments (which can be expressed as the derivatives of the moment-generating function evaluated at zero) easily follows from Cauchy’s integral formula.