Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T01:11:16.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals and derivatives of functions in MacLane's class 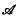and of normal functions†

Published online by Cambridge University Press:  24 October 2008

K. F. Barth  and
W. J. Schneider
K. F. Barth
Affiliation:
Syracuse University, Syracuse, N. Y.
W. J. Schneider
Affiliation:
Syracuse University, Syracuse, N. Y.
Get access Rights & Permissions [Opens in a new window]

Extract

If f is meromorphic in D = {,|z| < 1}, we say that f has the asymptotic value a at ζ, ζ ∈ C(={|z| = 1}), if there exists an arc Γ such that Γ ends at ζ, (Γ − {ζ}) ⊂ D, and f has the limit a as |z| → 1 on Γ. The class 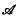(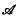M) originally defined by G. R. MacLane ((8), p. 8), consists of those functions that are non-constant and holomorphic (meromorphic) in D and that have asymptotic values at a dense subset of C. In (8), p. 36, MacLane has shown the following three conditions are sufficient for a non-constant holomorphic function f to be in :

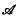Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 71 , Issue 1 , January 1972 , pp. 111 - 121
Copyright
Copyright © Cambridge Philosophical Society 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bagemihl, F. and Seidel, W.Some boundary properties of analytic functions. Math. Z. 61 (1954), 186–199.CrossRefGoogle Scholar
(2)Barth, K. F.Asymptotic values of meromorphic functions. Michigan Math. J. 13 (1966), 321–340.CrossRefGoogle Scholar
(3)Barth, K. F. and Schneider, W. J.On the impossibility of extending the Riesz uniqueness theorem to functions of slow growth. Ann. Acad. Sci. Fenn. (Ser. A. I) 432 (1968), 9 pp.Google Scholar
(4)Barth, K. F. and Schneider, W. J.Exponentiation of functions in MacLane's class . J. reine angew. Math. 236 (1969), 120–130.Google Scholar
(5)Hayman, W. K.On the characteristic of functions meromorphic in the unit disk and of their integrals. Acta Math. 112 (1964), 181–214.CrossRefGoogle Scholar
(6)Hayman, W. K.Meromorphic functions (Oxford University Press, London, 1964).Google Scholar
(7)Lehto, O. and Virtanen, K. I.Boundary behaviour and normal meromorphic functions. Acta Math. 97 (1957), 47–65.CrossRefGoogle Scholar
(8)MacLane, G. R.Asymptotic values of holomorphic functions, Rice Univ. Studies 49, 1 (1963), 1–83.Google Scholar
(9)MacLane, G. R. Exceptional values of f (n)(z), asymptotic values of f(z), and linearly accessible asymptotic values. (Mathematical Essays dedicated to A. J. MacIntyre, Ohio University Press, Athens, Ohio, 1970.)Google Scholar
(10)Mergelyan, S. N.On the representation of functions by series of polynomials on closed sets. (In Russian.) Dokl. Akad. Nauk SSSR 78 (1951), 405–408; Amer. Math. Soc. Transl. no. 85, Providence (1953).Google Scholar
(11)Schneider, W. J.An entire transcendental function whose inverse takes sets of finite measure into sets of finite measure. Bull. Amer. Math. Soc. 72 (1966), 841–842.CrossRefGoogle Scholar