No CrossRef data available.
Integral Invariants of the Affine Field
Published online by Cambridge University Press: 24 October 2008
Extract
In this paper the method of infinitesimal transformations of coordinates, used by Weyl to determine conditions that a function of the tensors gik and φi, and certain of their derivatives, should be a scalar density, is applied (with certain modifications so as to give tensor relations) to functions of 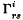 and
and 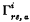 . It is known that in order that such a function should be a scalar density it must be a homogeneous function, of degree ½n, of
. It is known that in order that such a function should be a scalar density it must be a homogeneous function, of degree ½n, of 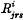 , and this must of course be deducible from the equations found by the infinitesimal transformations. In view of the part which these equations may play, as “equations of energy,” etc., in purely affine field theories, it seems desirable that the connection should be explicitly shown, and this is done in § 3.
, and this must of course be deducible from the equations found by the infinitesimal transformations. In view of the part which these equations may play, as “equations of energy,” etc., in purely affine field theories, it seems desirable that the connection should be explicitly shown, and this is done in § 3.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 3 , July 1926 , pp. 262 - 268
- Copyright
- Copyright © Cambridge Philosophical Society 1926
References
* Cf. Weitzenböck, Invariantentheorie, p. 358.
(after Schouten)
† Cf. Weyl, , Raum, Zeit, Materie, 5te Aufl., pp. 111, 309Google Scholar; also Weitzenböck, , op. cit., p. 372Google Scholar; Pauli, , Relativitätstheorie, §23.Google Scholar
* When r>s, ![]() and
and ![]() stand for
stand for ![]() and
and ![]() .
.
† A[rs]=½(Ars−Asr) (after Schouten).
* Of. Einstein, , “Zur allgemeinen Relativitätstheorie,” Sitzungsber. der Preuss. Akad., 1928, p. 35.Google Scholar


