Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T14:54:26.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Inhomogeneous random coverings of topological Markov shifts

Published online by Cambridge University Press:  22 June 2017

STÉPHANE SEURET
STÉPHANE SEURET*
Affiliation:
Université Paris-Est, LAMA (UMR 8050) UPEMLV, UPEC, CNRS F-94010, Créteil, France. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 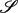$\mathscr{S}$ be an irreducible topological Markov shift, and let μ be a shift-invariant Gibbs measure on 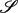$\mathscr{S}$. Let (Xn)n ≥ 1 be a sequence of i.i.d. random variables with common law μ. In this paper, we focus on the size of the covering of 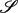$\mathscr{S}$ by the balls B(Xn, n−s). This generalises the original Dvoretzky problem by considering random coverings of fractal sets by non-homogeneously distributed balls. We compute the almost sure dimension of lim supn →+∞B(Xn, n−s) for every s ≥ 0, which depends on s and the multifractal features of μ. Our results include the inhomogeneous covering of 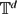$\mathbb{T}^d$ and Sierpinski carpets.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 165 , Issue 2 , September 2018 , pp. 341 - 357
Copyright
Copyright © Cambridge Philosophical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barral, J. and Seuret, S. Combining multifractal additive and multiplicative chaos. Commun. Math. Phys. 257 (2) (2005), 473–497.Google Scholar
[2] Barral, J. and Seuret, S. Heterogeneous ubiquitous systems in $\mathbb{R}^d$ and Hausdorff dimensions. Bull. Brazilian Math. Soc. 38 (3) (2007), 467–515.Google Scholar
[3] Barral, J. and Seuret, S. Ubiquity and large intersections properties under digit frequencies constraints. Math. Proc. Camb. Phil. Soc. 145 (3) (2008), 527–548.Google Scholar
[4] Barral, J., Ben Nasr, F. and Peyrière, J. Comparing multifractal formalisms: the neighbouring condition. Asian J. Math. 7 (2003), 149–166.Google Scholar
[5] Barral, J. and Fan, A.H. Covering numbers of different points in Dvoretzky covering. Bull. Sci. Math. 129 (2005), 275–317.Google Scholar
[6] Brown, G., Michon, G. and Peyrière, J. On the multifractal analysis of measures. J. Stat. Phys. 66 (1992), 775–790.Google Scholar
[7] Collet, P. and Koukiou, F. Large deviations for multiplicative chaos. Commun. Math. Phys. 147 (1992), 329–342.Google Scholar
[8] Collet, P., Lebowitz, J.L. and Porzio, A. The dimension spectrum of some dynamical systems. J. Stat. Phys. 47 (1987), 609–644.Google Scholar
[9] Dodson, M., Melián, M., Pestana, D. and Velani, S. Patterson measure and Ubiquity. Ann. Acad. Sci. Fenn. Ser. A I Math. 20 (1995), 37–60.Google Scholar
[10] Dvoretzky, A. On covering the circle by randomly placed arcs. Pro. Nat. Acad. Sci. USA 42 (1956), 199–203.Google Scholar
[11] Erdös, P. Some unsolved problems. Magyar Tud. Akad. Mat. Kutató Int. Közl. 6 (1961), 221–254.Google Scholar
[12] Fan, A. H., Feng, D. J. and Wu, J. Recurrence, dimension and entropy. J. London Math. Soc. 64 (1) (2001), 229–244.Google Scholar
[13] Fan, A. H., Schmeling, J. and Troubetzkoy, S. A multifractal mass transference principle for Gibbs measures with applications to dynamical Diophantine approximation. Proc. London Math. Soc. 107 (5) (2013), 1173–1219.Google Scholar
[14] Feng, D.J., Jarvenpäa, E., Jarvenpäa, M. and Suomala, V. Dimensions of random covering sets in Riemann manifolds. arXiv:1508.07881.Google Scholar
[15] Heurteaux, Y. Estimations de la dimension inférieure et de la dimension supérieure des mesures. Ann. Inst. H. Poincaré Probab. Statist. 34 (1998), 309–338.Google Scholar
[16] Jarvenpäa, E., Jarvenpäa, M., Koivusalo, H., Li, B. and Suomala, V. Hausdorff dimension of affine random covering sets in torus. Ann. Inst. Henri Poincaré Probab. Stat. 50 (4) (2014), 1371–1384.Google Scholar
[17] Jarvenpäa, E., Jarvenpäa, M., Koivusalo, B. Li, Suomala, V. and Xiao, Y. Hitting probabilities of random covering sets in torus and metric spaces. Preprint, arXiv: 1510.06630.Google Scholar
[18] Kahane, J.-P. Sur le recouvrement döun cercle par des arcs disposés au hasard C. R. Acad. Sci. Paris 248 (1956), 184–186.Google Scholar
[19] Kahane, J.-P. Some random series of functions Camb. Stud. Adv. Math. 5 (Cambridge University Press, 1985).Google Scholar
[20] Li, B., Shieh, N.R. and Xiao, Y. Hitting probability and packing dimensions of the random covering sets. In: Applications of Fractals and Dynamical Systems in Science and Economics (Carfi, David, Lapidus, Michel L., Pearse, Erin P. J. and van Frankenhuijsen, Machiel, editors). Amer. math. soc. (2013).Google Scholar
[21] Ojala, T., Suomala, V. and Wu, M. Random cutout sets with spatially inhomogeneous intensities. Preprint 2015.Google Scholar
[22] Olsen, L. A multifractal formalism. Adv. Math. 116 (1995), 92–195.Google Scholar
[23] Persson, T. A note on random coverings of Tori. Bull. London Math. Soc. 47 (1) (2015), 7–12.Google Scholar
[24] Ruelle, D. Thermodynamic formalism. The mathematical structures of classical equilibrium statistical mechanics. Encyclopedia of Mathematics and its Applications 5 (Addison-Wesley Publishing Co., Reading, Mass., 1978).Google Scholar
[25] Shepp, L. Covering the circle with random arcs. Israel J. Math. 11 (1972), 328–345.Google Scholar
[26] Tang, J. M. Random coverings of the circle with i.i.d. centers. Sci. China Math. 55 (6) (2015), 1257–1268.Google Scholar
[27] Tang, J. M. Hausdorff dimension of sets arising from Dvoretzky random covering. Acta. Mat. Sin. 57 (1) (2014).Google Scholar