Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T14:46:31.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite loop maps in geometric topology

Published online by Cambridge University Press:  24 October 2008

I. Madsen ,
V. Snaith  and
J. Tornehave
I. Madsen
Affiliation:
Matematisk Institut, Aarhus, University of Western Ontario, London, Canada
V. Snaith
Affiliation:
Matematisk Institut, Aarhus, University of Western Ontario, London, Canada
J. Tornehave
Affiliation:
Matematisk Institut, Aarhus, University of Western Ontario, London, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

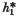0. Introduction. Let and 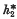be connected cohomology theories on the category of all CW spaces. In this paper we examine the relationship between natural homomorphisms (stable operations) of degree zero from 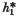to 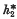and natural homomorphisms from 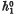to 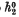in a number of cases of particular interest in topology – foremost the K-theories and the bundle theories classifying ‘surgery problems’. There are two parts to this. On the one hand we ask under what conditions a homomorphism from 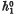to 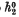extends to a stable operation and on the other hand when is a stable operation determined by its restriction to .

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 81 , Issue 3 , May 1977 , pp. 399 - 430
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Adams, J. F.On the groups J(X) I–-IV. Topology 2 (1963); 3 (1964), 137–171, 193–222; 5 (1966), 21–71.Google Scholar
(2)Adams, J. F.Lectures on generalized cohomology, Category Theory, Homology Theory and their applications, vol II (Lecture Notes in Mathematics, no. 99, Springer-Verlag, 1969).Google Scholar
(3)Adams, J. F.Stable homotopy and generalized homology (Lecture notes, University of Chicago, 1971).Google Scholar
(4)Adams, J. F. and Priddy, S. (to appear).Google Scholar
(5)Anderson, D. W. Thesis, University of California, Berkeley (1964).Google Scholar
(6)Anderson, D. W. and Hodgkin, L.The K-theory of Eilenberg-MacLane complexes. Topology.Google Scholar
(7)Atiyah, M. F.Characters and cohomology of finito groups, Publ. Math. Inst. des Hautes Études Sci. 9 (1961), 23–64.CrossRefGoogle Scholar
(8)Atiyah, M. F.Power operations in K-theory. Quart. J. Math. 17 (1966), 165–193.Google Scholar
(9)Atiyah, M. F., Bott, R. and Shapiro, A.Clifford modules. Topology 3 ( Suppl. 1) (1964), 3–38.Google Scholar
(10)Atiyah, M. F. and Segal, G. B.Exponential isomorphisms for λ-rings. Quart. J. Math. 22 (1971), 371–378.Google Scholar
(11)Atiyah, M. F. and Segal, G. B.Equivariant K-theory and completion. J. Differential Geometry 3 (1969), 1–18.CrossRefGoogle Scholar
(12)Atiyah, M. F. and Tall, D. O.Group representations, λ-rings and the J-homomorphism. Topology 8 (1969), 253–297.Google Scholar
(13)Boardman, J. M. and Vogt, R. M.Homotopy invariant algebraic structures on topological spaces (Lecture Notes in Mathematics, no. 347, Springer-Verlag, 1973).Google Scholar
(14)Hodgkin, L.The K-theory of some more well-known spaces. I. Q(S 0). Topology 11 (1972), 371–375.Google Scholar
(15)Hodgkin, L. and Snaith, V. P. The K-theory of some more well-known spaces (to appear).Google Scholar
(16)Kahn, D. S. and Priddy, S. B.Applications of the transfer to stable homotopy theory. Bull Amer. Math. Soc. 76 (6) (1972), 981–987.CrossRefGoogle Scholar
(17)Kervaire, M. and Milgram, J.Groups of homotopy Spheres: I. Ann. of Math. 77 (1963), 504–537.Google Scholar
(18)Madsen, I. and Milgram, R. J. The oriented bordism of topological manifolds and integrality relations (To appear.)Google Scholar
(19)May, J. P.The geometry of iterated loop spaces (Lecture Notes in Mathematics, no. 271, Springer-Verlag, 1972).Google Scholar
(20)May, J. P. (with contributions by F. Quinn and N. Ray). E∞ ring spaces and E∞ ring spectra.Google Scholar
(21)Milnor, J.On axiomatic homology theory. Pacific. J. Math. 12 (1962), 337–341.Google Scholar
(22)Nöbeling, G.Uber die Derivierten des inversen und des direkten Limes einer Modulfamilie. Topology 1 (1961), 47–61.CrossRefGoogle Scholar
(23)Segal, G. B.Categories and cohomology theories. Topology 13 (1974), 293–312.Google Scholar
(24)Segal, G. B.The representation ring of a compact Lie group. Inst. des Hautes Études Sci. (1968), 113–128.Google Scholar
(25)Seymour, R. M.Vector bundles invariant under the Adams operations. Quart. J. Math. 25 (1974),395–414.Google Scholar
(26)Snaith, V. P. Splitting of the image of the J-homomorphism. (To appear.)Google Scholar
(27)Stung, R.Cobordism (Lecture Notes in Mathematics, Princeton University Press, 1968).Google Scholar
(28)Sullivan, D. Triangulating homotopy equivalences (Mimeographed notes, Warwick University, 1966).Google Scholar
(29)Sullivan, D. Geometric topology, part I (Mimeographed notes, M.I.T. 1970).Google Scholar
(30)Sullivan, D.Genetics of homotopy theory and the Adams conjecture. Ann. of Math. 100 (1974), 1–80.Google Scholar
(31)Tornehave, J. The splitting of spherical fibration theory (preprint, Aarhus, 1973).Google Scholar
(32)Tornehave, J. The Brauer lifting is an infinite loop map. (To appear.)Google Scholar
(33)Hirsch, M. and Mazur, B.Smoothings of piecewise linear manifolds. Ann of Math. Studies 80, Princeton 1974.Google Scholar
(34)Cerf, J.Sur les diffeomorphismes de la sphère de dimensions trois (Γ4 = 0) (Lecture Notes in Mathematics, no. 53, Springer-Verlag, 1968).Google Scholar