Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yamagishi, Kikumichi
1991.
Bass number characterization of surjective Buchsbaum modules.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 2,
p.
261.
Yamagishi, Kikumichi
1994.
Type of blowing-up over a Buchsbaum ring.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 3,
p.
407.
Yoshida, Ken-ichi
1995.
On linear maximal buchsbaum modules and the syzygy modules.
Communications in Algebra,
Vol. 23,
Issue. 3,
p.
1085.
Kurano, Kazuhiko
and
Yamagishi, Kikumichi
1997.
On Macaulayfication Obtained by a Blow-Up Whose Center Is an Equi-Multiple Ideal.
Journal of Algebra,
Vol. 190,
Issue. 2,
p.
405.
Nakamura, Yukio
1998.
On the Buchsbaum Property of Associated Graded Rings.
Journal of Algebra,
Vol. 209,
Issue. 1,
p.
345.
Watanabe, Kei-ichi
and
Yoshida, Ken-ichi
2000.
Hilbert–Kunz Multiplicity and an Inequality between Multiplicity and Colength.
Journal of Algebra,
Vol. 230,
Issue. 1,
p.
295.
Shimoda, Yasuhiro
and
Yamagishi, Kikumichi
2000.
On the Buchsbaum Associated Graded Modules with Respect to m-Primary Ideals Whose Reduction Numbers Are at Most One.
Journal of Algebra,
Vol. 234,
Issue. 1,
p.
169.
Yamagishi, Kikumichi
2000.
The associated graded modules of Buchsbaum modules with respect to m-primary ideals in the equi-II-invariant case.
Journal of Algebra,
Vol. 225,
Issue. 1,
p.
1.
Yamagishi, Kikumichi
2002.
Buchsbaumness in Rees Modules Associated to Ideals of Minimal Multiplicity in the Equi-I-Invariant Case.
Journal of Algebra,
Vol. 251,
Issue. 1,
p.
213.
Yamagishi, Kikumichi
2003.
Buchsbaumness in the Rees modules associated to m-primary ideals in the one-dimensional case.
Journal of Pure and Applied Algebra,
Vol. 181,
Issue. 2-3,
p.
309.
Goto, Shiro
and
Yoshida, Ken-ichi
2007.
Buchsbaum homogeneous algebras with minimal multiplicity.
Journal of Pure and Applied Algebra,
Vol. 210,
Issue. 3,
p.
735.
Yamagishi, Kikumichi
2009.
Buchsbaumness of certain generalization of the associated graded modules in the equi-I-invariant case.
Journal of Algebra,
Vol. 322,
Issue. 8,
p.
2861.
Anderson, D. D.
and
Winders, M.
2009.
Idealization of a Module.
Journal of Commutative Algebra,
Vol. 1,
Issue. 1,
Nguyen, Thi Hong Loan
and
Nong, Quoc Chinh
2013.
IDEALIZATIONS OF PSEUDO BUCHSBAUM MODULES OVER A PSEUDO BUCHSBAUM RING.
Bulletin of the Korean Mathematical Society,
Vol. 50,
Issue. 5,
p.
1523.
Hong Loan, Nguyen
2014.
On certain invariants of idealizations.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 51,
Issue. 3,
p.
357.
LOAN, NGUYEN THI HONG
2014.
PSEUDO BUCHSBAUMNESS FOR IDEALIZATIONS OF NOETHERIAN MODULES OVER LOCAL RINGS.
Journal of Algebra and Its Applications,
Vol. 13,
Issue. 02,
p.
1350084.
Loan, Nguyen Thi Hong
2017.
On canonical modules of idealizations.
Journal of Commutative Algebra,
Vol. 9,
Issue. 1,
Nam, Pham Hong
2024.
ON THE PARTIAL EULER–POINCARÉ CHARACTERISTICS OF KOSZUL COMPLEXES OF IDEALIZATION.
Journal of Commutative Algebra,
Vol. 16,
Issue. 1,


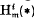 stands for the
stands for the 