Published online by Cambridge University Press: 24 October 2008
Let Γ be a discrete group. Γ is said to have finite virtual cohomological dimension (vcd) if there exists a finite index torsion-free subgroup Γ' of Γ such that Γ' has finite cohomological dimension over 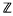 . Examples of such groups include the fundamental group of a finite graph of finite groups, arithmetic groups, mapping class groups and outer automorphism groups of free groups. One of the fundamental problems in topology is to understand the cohomology of these finite vcd-groups.
. Examples of such groups include the fundamental group of a finite graph of finite groups, arithmetic groups, mapping class groups and outer automorphism groups of free groups. One of the fundamental problems in topology is to understand the cohomology of these finite vcd-groups.