Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T19:17:48.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Hermitian character and the first problem for R. H. Fox for links

Published online by Cambridge University Press:  24 October 2008

Adrian Pizer
Adrian Pizer
Affiliation:
Department of Mathematics, Osaka City University, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

The fundamental group G of a μ-component link has the properties:

(1) G is finitely presented, with deficiency 1;

(2) G/G′ is free abelian on μ distinguished generators, say {t1 …, tμ}.

Let ψ: G → G/G′ → 〈t〉 be the composition of the canonical projection G → G/G′ and the epimorphism defined by 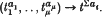. Then the Z〈t〉-module M = Ker ψ/(Ker ψ)′ (the so-called module of the link) has a square (say n × n) relation matrix N. We write [N] for the Z〈t〉-equivalence class of N (Fox [3], p. 199) and N′̅ for the conjugate transpose of N.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 1 , July 1987 , pp. 77 - 86
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Crowell, R. H.. The group G′/G′′ of a knot group G. Duke Math. J. 30 (1963), 349–354.Google Scholar
[2] Crowell, R. H. and Fox, R. H.. Introduction to Knot Theory (Ginn Blaisdell, 1963).Google Scholar
[3] Fox, R. H.. Free differential calculus 2. Ann. of Math. 59 (1954), 196–210.CrossRefGoogle Scholar
[4] Fox, R. H.. Some problems in knot theory. Topology of 3-Manifolds and Related Topics, ed. Fort, M. K. Jr (Prentice-Hall, 1962), 168–176.Google Scholar
[5] Jans, J. P.. Rings and Homology. Selected Topics in Mathematics, Athena Series (Holt, Rinehart and Winston, 1964).Google Scholar
[6] Kawauchi, A.. A test for the fundamental group of a 3-manifold. J. Pure Appl. Algebra 28 (1983), 189–196.CrossRefGoogle Scholar
[7] Kawauchi, A.. On critical points of proper surfaces in the upper half 4-space (unpublished version). Osaka City University (1984).Google Scholar
[8] Kawauchi, A.. On the integral homology of infinite cyclic coverings of links. Kobe J. Math. (in the Press).Google Scholar
[9] Kawauchi, A.. Integral torsion in the infinite cyclic covering homology of a ribbon link. To appear (in Japanese).Google Scholar
[10] Kearton, C.. Blachfield duality and simple knots. Trans. Amer. Math. 202 (1975), 141–160.CrossRefGoogle Scholar
[11] Keef, P. W.. On the S-equivalence of some general sets of matrices. Rocky Mtn. J. Math. 13 (1983), 541–551.CrossRefGoogle Scholar
[12] Lang, S.. Algebra (Addison-Wesley World Student Series Edition, 2nd printing, 1970).Google Scholar
[13] Newman, M.. Integral Matrices. Pure and Applied Mathematics Series, vol. 45 (Academic Press, 1972).Google Scholar
[14] O'meara, O. T.. Introduction to quadratic forms. Grundlehren Math. Wiss. 117 (Springer-Verlag, 1963).Google Scholar
[15] Pizer, A.. Matrices over group rings which are Alexander matrices. Osaka J. Math. 21 (1984), 461–472.Google Scholar
[16] Pizer, A.. Hermitian character and the first problem of R. H. Fox. Math. Proc. Cambridge Philos. Soc. 98 (1985), 447–458.CrossRefGoogle Scholar
[17] Rolfsen, D.. Knots and Links (Publish or Perish Inc., 1976).Google Scholar
[18] Rotman, J. J.. An Introduction to Homological Algebra. Pure and Applied Math. Series, 85 (Academic Press, 1979).Google Scholar
[19] Schreier, O. and Sperner, E.. Modern Algebra and Matrix Theory (Chelsea Publishing Co., 1951).Google Scholar
[20] Seifert, H.. Über das Geschlect von Knoten. Math. Ann. 110 (1934), 571–592.CrossRefGoogle Scholar
[21] Seshadri, C. S.. Triviality of vector bundles over the affine space K2. Proc. Nat. Acad. Sci. U.S.A. 44 (1958), 456–458.CrossRefGoogle ScholarPubMed
[22] Swan, R. G.. Protective modules over Laurent polynomial rings. Trans. Amer. Math. Soc. 237 (1978), 111–120.CrossRefGoogle Scholar
[23] Torres, G.. On the Alexander polynomial. Ann. of Math. 59 (1953), 57–89.CrossRefGoogle Scholar
[24] Torres, G. and Fox, R. H.. Dual presentations of the group of a knot. Ann. of Math. 59 (1954), 211–218.CrossRefGoogle Scholar
[25] Trotter, H. F.. On S-equivalence of Seifert matrices. Inventiones Math. 20 (1973), 173–207.CrossRefGoogle Scholar
[26] Trotter, H. F.. Torsion free metabelian groups with infinite cyclic quotient groups. Proc. 2nd Int. Conf. Theory of groups. Lecture Notes in Math. vol. 372 (Springer-Verlag, 1973), 655–666.Google Scholar
[27] Trotter, H. F.. Knot modules and Seifert matrices. Knot Theory. Lecture Notes in Math. vol. 685 (Springer-Verlag, 1977), 291–299.CrossRefGoogle Scholar