Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T13:28:34.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic maps from surfaces into pseudo-Riemannian spheres and hyperbolic spaces

Published online by Cambridge University Press:  24 October 2008

S. Erdem
S. Erdem
Affiliation:
University of Leeds
Get access Rights & Permissions [Opens in a new window]

Extract

In [2, 4, 5, 6, 7] Calabi, Barbosa and Chern showedthat there is a 2:1 correspondence between arbitrary pairs of full isotropic (terminology as in [8]) harmonic maps ±φ:M→S2m from a Riemann surface to a Euclidean sphere and full totally isotropic holomorphic maps f:M→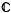2m from the surface to complex projective space. In this paper we show, very explicitly, how to construct a similar one-to-one correspondence when S2m is replaced by some other space forms of positive and negative curvatures with their standard (indefinite) metrics obtained by restricting a standard (indefinite) bilinear form on Euclidean space to the tangent spaces. We get over a difficulty encountered by Barbosa of dealing with the zeros of a certain wedge product by a technique adapted from [8]. The case of complex projective space forms (indefinite complex projective and complex hyperbolic spaces) will be considered in a separate paper. Some further developments in classification theorems are given by Eells and Wood [8], Rawnsley[14], [15] and Erdem and Wood [10].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 94 , Issue 3 , November 1983 , pp. 483 - 494
Copyright
Copyright © Cambridge Philosophical Society 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baird, P.. Harmonic maps with symmetry, harmonic morphisms and deformations of metrics. Ph.D. thesis, Warwick University, 1981.Google Scholar
[2] Barbosa, J.. On minimal immersions of S 2 into S 2m. Trans. Amer. Math. Soc. 210 (1975), 75–106.Google Scholar
[3] Borchers, H. J. and Garber, W. D.. Local theory of solutions for the 0(2k+1)-model. Comm. Math. Phys. 72 (1980), 77–102.CrossRefGoogle Scholar
[4] Calabi, E.. Minimal immersions of surfaces in Euclidean spheres. J. Differential Geom. 1 (1967), 111–125.CrossRefGoogle Scholar
[5] Calabi, E.. Quelques applications de l'analyse complexe aux surfaces d'aire minima. In Topics in Complex Manifolds (University of Montreal, 1967), 59–81.Google Scholar
[6] Chern, S. S.. On the minimal immersions of the two-sphere in a space of constant curvature. Problems in Analysis (Princeton University Press, 1970), 27–40.Google Scholar
[7] Chern, S. S.. On minimal spheres in the four sphere. In Studies and Essays Presented to Y. W. Chen (Taiwan, 1970), 137–150.Google Scholar
[8] Eells, J. and Wood, J. C.. Harmonic maps from surfaces to complex projective spaces. Adv. in Math. (In the Press.)Google Scholar
[9] Eells, J. and Sampson, J. H.. Harmonic mappings of Riemannian manifolds. Amer. J. Math. 86 (1964), 109–159.CrossRefGoogle Scholar
[10] Erdem, S. and Wood, J. C.. On the construction of harmonic maps into a Grassmannian. J. London Math. Soc. (1983). (In the Press.)CrossRefGoogle Scholar
[11] Kobayashi, S. and Nomizu, K.. Foundations of Differential Geometry, vol. I, II (Wiley Interscienee, 1963, 1969).Google Scholar
[12] Koszul, J. L. and Malorange, B.. Sur certaines structure fibrés complexes. Arch. Math. 9 (1958), 102–109.CrossRefGoogle Scholar
[13] Petrowski, I.. Sur l'analyticité des solutions des systèmes d'équations différentielles. Mat. Sb. (N.S.) 5 (47), (1939), 3–70.Google Scholar
[14] Rawnsley, J. H.. On the rank of horizontal maps. Math. Proc. Cambridge Philos. Soc. 92 (1982), 485–488.CrossRefGoogle Scholar
[15] Rawnsley, J. H.. Notes on Homogeneous Spaces. (Preprint, University of Warwick, 1982.)Google Scholar
[16] Wolf, J. A.. Spaces of Constant Curvature (McGraw-Hill, 1967).Google Scholar
[17] Wood, J. C.. Harmonic Maps and Complex Analysis, Proc. Summer Course in Com plex Analysis, vol. III (Trieste, 1976), pp. 289–308.Google Scholar
[18] Wu, H.. The Equidistribution Theory of Holomorphic Curves. Annals of Mathematics Studies, no. 64 (Princeton University Press, 1970).CrossRefGoogle Scholar