Published online by Cambridge University Press: 24 October 2008
Two recent papers have discussed eigenvalue problems relating to second-order, self-adjoint differential equations from the point of view of the deferred approach to the limit in the finite-difference treatment of the problem. In both cases the problem is made definite by considering the differential equation
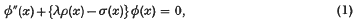
primes denoting differentiation with respect to x, with two-point boundary conditions

and given at the ends of the interval (0, 1). The usual finite-difference approach is to divide the range (0, 1) into N equal strips of length h = 1/N, giving a set of N + 1 pivotal values φn as the analogue of a solution of (1), φn denoting the pivotal value at x = nh. In terms of central differences we then have
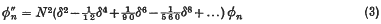
and retaining only second differences yields a finite-difference approximation φn = Un to (1), where the pivotal U-values satisfy the equations
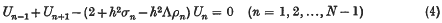
defined at all internal points, together with two equations holding at the end-points and approximately satisfying the end conditions (2). Here Λ is the corresponding approximation to the eigenvalue λ. A possible finite-difference treatment of the end conditions (2) would be to replace (1) at x = 0 by the central-difference formula
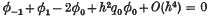
and use the corresponding result for the first derivative of φ, i.e.
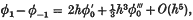
whereq(x) = λρ(x) – σ(x). Eliminating the external value φ–1 between these two and making use of (1) and (2) we obtain the equation
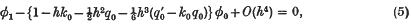
where for convenience we write k0 = B0/A0. Similarly at x = 1 we obtain
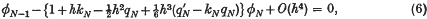
withkN = B1/A1. If we neglect terms in h3 in these two they become what are usually taken to be the first approximation to the end conditions (2) to be used in conjunction with the set (4) (with the appropriate change φ = U, λ = Λ). This, however, results in a loss of accuracy at the end-points over the general level of accuracy of the set (4), which is O(h4), so there is some justification for retaining the terms in h3, e.g. if a difference correction method were being used they would subsequently be added as a correction term.