The geometric realization of Wall obstructions by nilpotent and simple spaces
Published online by Cambridge University Press: 24 October 2008
Extract
Let π denote a finite group. It is well known that every element of the projective class group K0 ℤπ may be realized as Wall obstruction of a finitely dominated complex with fundamental group π (cf. (13)). We will study two subgroups N0ℤπ and Nℤπ of K0ℤπ, which are closely related to the Wall obstruction of nilpotent spaces. If the group π is nilpotent and if S denotes the set of elements x ∈ K0ℤπ which occur as Wall obstructions of nilpotent spaces, then
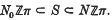
It turns out that in many instances one has N0,ℤπ = Nℤπ (cf. Section 3) and one obtains hence new information on S. The main theorem (2·4) provides a systematic way of constructing finitely dominated nilpotent (or even simple) spaces with non-vanishing Wall obstructions.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 87 , Issue 2 , March 1980 , pp. 199 - 206
- Copyright
- Copyright © Cambridge Philosophical Society 1980
References
REFERENCES
- 3
- Cited by


