The generalized Fermi interaction
Published online by Cambridge University Press: 24 October 2008
Extract
Konopinski and Uhlenbeck have shown that the empirical β-ray spectra seem to require a modification of Fermi's original expression for the interaction leading to β decay‡. Their expression includes a derivative of the neutrino wave function. The purpose of the present paper is to investigate the most general type of such an interaction term and the possibility of introducing second-order derivatives. We have to deal with the transition§
neutron + neutrino → proton + electron
or proton + anti-neutrino → neutron + positron.
The whole system has the equations of motion
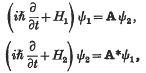
where ψ1 and ψ2 are the wave functions of the initial and final states in configuration space, H1 and H2 are the Hamiltonians of the particles in the initial and final states, and A is a small interaction operator.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 33 , Issue 2 , April 1937 , pp. 277 - 292
- Copyright
- Copyright © Cambridge Philosophical Society 1937
References
‡ Fermi, , Zeit. f. Physik, 88 (1934), 161;CrossRefGoogle ScholarKonopinski, and Uhlenbeck, , Phys. Rev. 48 (1935), 7.CrossRefGoogle Scholar The latter paper will be quoted as K.–U.
§ Following K.–U. we choose this more symmetric description of the process, in which the emission of an anti-neutrino is replaced by the absorption of a neutrino from a state of negative energy and vice versa.
‡ Bethe, and Bacher, , Rev. Mod. Phys. 8 (1936), 190.CrossRefGoogle Scholar By pseudo-vector or pseudo-vector or pseudoscalar we mean quantities which transform like vectors or scalars under Lorentz transformations of determinant +1 but change sign if the transformation determinant is −1.
§ Such an expression was actually proposed by Weizäcker, , Zeit. f. Physik, 102 (1936), 572,CrossRefGoogle Scholar and it seems therefore rather too special to exclude linear combinations as in the treatment of Bethe and Bacher.
‡ Kurie, , Richardson, and Paxton, , Phys. Rev. 49 (1936), 368.CrossRefGoogle Scholar
‡ Lyman, , Phys. Rev. 51 (1937), 1.CrossRefGoogle Scholar
‡ For a = b the 00 component of the interaction term becomes
This is W 0 times the K.–U. interaction, and similarly we could introduce n + 1 derivative such as ![]()
* Bethe, and Bacher, , Rev. Mod. Phys. 8 (1936), 201.CrossRefGoogle Scholar
- 4
- Cited by


