Galois theory of Salem polynomials

Abstract

Let f(x) ∈ 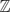[x] be a monic irreducible reciprocal polynomial of degree 2d with roots r₁, 1/r₁, r₂, 1/r₂, . . ., r_d, 1/r_d. The corresponding trace polynomial g(x) of degree d is the polynomial whose roots are r₁ + 1/r₁, . . ., r_d + 1/r_d. If the Galois groups of f and g are G_f and G_g respectively, then G_g ≅ G_f/N, where N is isomorphic to a subgroup of C₂^d. In a naive sense, the generic case is G_f ≅ C₂^d ⋊ S_d, with N ≅ C₂^d and G_g ≅ S_d. When f(x) has extra structure this may be reflected in the Galois group, and it is not always true even that G_f ≅ N ⋊ G_g. For example, for cyclotomic polynomials f(x) = Φ_n(x) it is known that G_f ≅ N ⋊ G_g if and only if n is divisible either by 4 or by some prime congruent to 3 modulo 4.

In this paper we deal with irreducible reciprocal monic polynomials f(x) ∈ 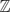[x] that are ‘close’ to being cyclotomic, in that there is one pair of real positive reciprocal roots and all other roots lie on the unit circle. With the further restriction that f(x) has degree at least 4, this means that f(x) is the minimal polynomial of a Salem number. We show that in this case one always has G_f ≅ N ⋊ G_g, and moreover that N ≅ C₂^d or C₂^d−1, with the latter only possible if d is odd.