Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alexander, J. C.
and
Fitzpatrick, P. M.
1981.
Fixed Point Theory.
Vol. 886,
Issue. ,
p.
1.
Alexander, J. C.
and
Antman, Stuart S.
1981.
Global and local behavior of bifurcating multidimensional continua of solutions for multiparameter nonlinear eigenvalue problems.
Archive for Rational Mechanics and Analysis,
Vol. 76,
Issue. 4,
p.
339.
Alexander, J. C.
1981.
Fixed Point Theory.
Vol. 886,
Issue. ,
p.
455.
Welsh, Stewart C.
1987.
Bifurcation of A-proper mappings without transversality considerations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 107,
Issue. 1-2,
p.
65.
Fitzpatrick, P.M.
1988.
Homotopy, linearization, and bifurcation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 12,
Issue. 2,
p.
171.
Healey, Timothy J.
1988.
Global Bifurcations and Continuation in the Presence of Symmetry with an Application to Solid Mechanics.
SIAM Journal on Mathematical Analysis,
Vol. 19,
Issue. 4,
p.
824.
Welsh, Stewart C.
1988.
Global results concerning bifurcation for Fredholm maps of index zero with a transversality condition.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 12,
Issue. 11,
p.
1137.
Fitzpatrick, P. M.
and
Pejsachowicz, Jacobo
1991.
Parity and generalized multiplicity.
Transactions of the American Mathematical Society,
Vol. 326,
Issue. 1,
p.
281.
Welsh, Stewart C.
1995.
A vector parameter global bifurcation result.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 25,
Issue. 12,
p.
1425.
Welsh, Stewart C.
2005.
A generalized-degree homotopy yielding global bifurcation results.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 62,
Issue. 1,
p.
89.
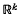 , k a positive integer. The basic contribution is that the parameter is vector valued and that the nonlinearities allowed are very general; however, even for scalar parameters, our results extend those of previous authors.
, k a positive integer. The basic contribution is that the parameter is vector valued and that the nonlinearities allowed are very general; however, even for scalar parameters, our results extend those of previous authors.

