Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T13:14:00.679Z Has data issue: false hasContentIssue false
  • English
  • Français

A further instability theorem for a certain fifth-order differential equation

Published online by Cambridge University Press:  24 October 2008

J. O. C. Ezeilo
J. O. C. Ezeilo
Affiliation:
University of Nigeria, Nsukka, Nigeria
Get access Rights & Permissions [Opens in a new window]

Extract

In our previous consideration in (1) of the constant-coefficient fifth-order differential equation:

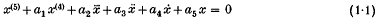
an attempt was made to identify (though not exhaustively) different sufficient conditions on a1,…,a5 for the instability of the trivial solution x = 0 of (1·1). It was our expectation that the conditions so identified could be generalized in some form or other to equations (1·1) in which a1,…,a5 were not necessarily constants, thereby giving rise to instability theorems for some non-linear fifth-order differential equations; and this turned out in fact to be so except only for the case:

with R0 = R0(a1, a2, a3, a4) > 0 sufficiently large, about which we were unable at the time to derive any worthwhile generalization to any equation (1·1) in which a1, …,a5 are not all constants.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 3 , November 1979 , pp. 491 - 493
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

(1)Ezeilo, J. O. C.Math. Proc. Cambridge Philos. Soc. 84 (1978), 343–350.Google Scholar