Published online by Cambridge University Press: 24 October 2008
It is trivial that the fundamental equations of electromagnetism are invariant under orthogonal transformations of space. This invariance can be brought into evidence by using the calculus adapted to the orthogonal group, viz. the vector-calculus. The equations can be written either in their integral form
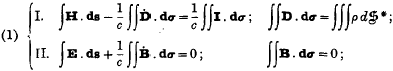
or in their differential form
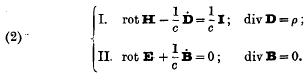
* The line-element ds is considered as an infinitesimal vector, tangent to the curve; the surface-element dσ as an infinitesimal vector normal to the surface. The space-element is denoted by dS, the space-time element by dΣ.
* The indices h, i, j, k, l, m run through the values 1, 2, 3, 4.
† Cf. Cunningham, E., Proc. London Math. Soc. (2), 8 (1910), 77–98CrossRefGoogle Scholar; Bateman, H., ibidem 8 (1910), 223–264, 469–488Google Scholar; 21 (1920), 256–270. Compare also: Bessel-Hagen, E., “Über die Erhaltungssätze der Elektrodynamik,” Math. Ann. 84 (1921), 258–276.CrossRefGoogle Scholar
‡ Schouten, J. A. and Haantjes, J., “Über die konforminvariante Gestalt der Maxwellschen Gleichungen und der elektromagnetischen Impulsenergiegleich-ungen,” Physica, 1 (1934), 869–872CrossRefGoogle Scholar ("Konforme Feldtheorie i").
§ The indices a, b, c, d, e, f, g will run through the values 1, 2, 3 only.
* a ab is the fundamental tensor of space: a ab = g ab. Note that a ab is negative definite.
† e′abc is the covariant unity trivector:
e abc is the contravariant unity trivector:
Hence e′abc = − e abc, where the indices are lowered with the aid of a ab.
‡ Space coordinates are denoted by ξa, space-time coordinates by ξi. For orthogonal coordinates we have ![]()
§ We use, with Schouten, square brackets to denote the alternated part of an affinor, e.g.
∥ Compare, however, the equivalent form, mentioned below.
* Hence ![]()
* The following identities (formulated for n-vector densities in n-dimensional space) are often used in computations:
where ![]() is defined by
is defined by
In particular, we often use

† The equation I = λE is irrelevant, since it is only an asymptotic condition, valid for stationary currents.
* I hope to return to this question on a later occasion.
† It might seem that by means of ηijkl metric (though a generalized form of it) is introduced in the theory again. This, however, is not the case: in the ordinary theory matter is characterized by μab, εab and metric by a ab; they all occur in the formulae (1), (14). We only use ηijkl which characterizes matter, but has nothing to do with ordinary metric, except in special cases. It defines a kind of conformal metric for surface-elements dσ ij, determined by the scalar density of weight − 1
If and only if ηijkl degenerates according to (27) this conformal metric can be extended to a conformal metric for line-elements dξ i, determined by the scalar density of weight ![]()
Nevertheless in permeable or dielectric matter these metrics are still independent of the ordinary conformal metric, which is merely an extrapolation of the conformal metric of free ether into matter, so that we do not return to the dualistic standpoint of ordinary electrodynamics.