Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T16:27:38.240Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions and applications of a tauberian theorem due to valiron

Published online by Cambridge University Press:  24 October 2008

M. E. Noble
M. E. Noble
Affiliation:
Queen's CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. Introduction. In the course of an important memoir on integral functions of finite order†, G. Valiron discusses ‘fonctions orientées’, that is, functions with zeros an such that arg an tends to a limit as n → ∞. He obtains results that include the following two theorems, in which Vρ(x) denotes a function of the form 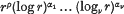, where α1, …, αν are positive integers, and n(r) has its usual significance in the theory of integral functions:.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 1 , January 1951 , pp. 22 - 37
Copyright
Copyright © Cambridge Philosophical Society 1951

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Ann. Fac. Sci. Toulouse (3), 5 (1914), 117.Google Scholar

‡ Proc. London Math. Soc. (2), 26 (1926–1947), 185.Google Scholar

§ Quart. J. Math. 19 (1948), 90.Google Scholar

∥ Ann. Math. 49 (1948), 200, 533.Google Scholar

C.R. Acad. Sci., Paris, 228 (1948), 1365.Google Scholar

† Titchmarsh, E. C., Theory of functions (Oxford, 1932), p. 271.Google Scholar

† Valiron, G., Integral functions (Toulouse, 1923), pp. 65–7.Google Scholar

‡ Bull. Soc. Math. France, 35 (1907).Google Scholar

† Proc. London Math. Soc. (2), 38 (1935), 178–9.Google Scholar