Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T16:38:49.635Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates of Zeros of a Polynomial

Published online by Cambridge University Press:  24 October 2008

L. Mirsky
L. Mirsky
Affiliation:
Department of Pure MathematicsUniversity of Sheffield
Get access Rights & Permissions [Opens in a new window]

Extract

Throughout this note we shall consider a fixed polynomial 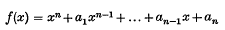with complex coefficients and of degree n ≥ 2. Its zeros will be denoted by ξ1, ξ2, …, ξn where the numbering is such that 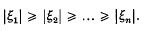Making use of Jensen's integral formula, Mahler (4) showed that, for l ≥ k < n, 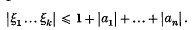A slightly weaker result had been established by Feldman in an earlier publication (2). Mahler's inequality (1) is of importance in the study of transcendental numbers, and our first object is to sharpen his bound by proving the following result.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 2 , April 1962 , pp. 229 - 234
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Courant, R. and Hilbert, D.Methoden der mathematischen Physik (Berlin, 1931).CrossRefGoogle Scholar
(2)Feldman, N. I.Approximation of certain transcendental numbers (I). Izv. Akad. Nauk SSSR, Ser. Math. 15 (1951), 53–74.Google Scholar
(3)Frobenius, G.Über Matrizen aus positiven Elementen. Sitzb. Preuss. Akad. Wiss. (1908), 471–476.Google Scholar
(4)Mahler, K.An application of Jensen's formula to polynomials. Mathematika, 7 (1960), 98–100.CrossRefGoogle Scholar
(5)Newman, D. J.Zeros of a special polynomial. American Math. Monthly, 68 (1961), 387–388.CrossRefGoogle Scholar
(6)Perron, O.Algebra (2nd ed.; Berlin and Leipzig, 1932–1933).Google Scholar
(7)Rados, O.Zur Theorie der adjungierten Substitutionen. Math. Ann. 48 (1897), 417–424.CrossRefGoogle Scholar
(8)Turnbull, H. W. and Aitken, A. C.An introduction to the theory of canonical matrices (London and Glasgow, 1948).Google Scholar
(9)Weyl, H.Inequalities between the two kinds of eigenvalues of a linear transformation. Proc. Nat. Acad. Sci. U.S.A. 35 (1949), 408–411.CrossRefGoogle ScholarPubMed