Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T02:30:23.687Z Has data issue: false hasContentIssue false
  • English
  • Français

The Erdős–Rothschild problem on edge-colourings with forbidden monochromatic cliques

Published online by Cambridge University Press:  23 January 2017

OLEG PIKHURKO ,
KATHERINE STADEN  and
ZELEALEM B. YILMA
OLEG PIKHURKO
Affiliation:
Mathematics Institute and DIMAP, University of Warwick, Coventry, CV4 7AL. e-mail: [email protected], [email protected]
KATHERINE STADEN
Affiliation:
Mathematics Institute and DIMAP, University of Warwick, Coventry, CV4 7AL. e-mail: [email protected], [email protected]
ZELEALEM B. YILMA
Affiliation:
Carnegie Mellon University Qatar, Doha, Qatar. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let k := (k1,. . .,ks) be a sequence of natural numbers. For a graph G, let F(G;k) denote the number of colourings of the edges of G with colours 1,. . .,s such that, for every c ∈ {1,. . .,s}, the edges of colour c contain no clique of order kc. Write F(n;k) to denote the maximum of F(G;k) over all graphs G on n vertices. This problem was first considered by Erdős and Rothschild in 1974, but it has been solved only for a very small number of non-trivial cases.

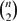We prove that, for every k and n, there is a complete multipartite graph G on n vertices with F(G;k) = F(n;k). Also, for every k we construct a finite optimisation problem whose maximum is equal to the limit of log2F(n;k)/${n\choose 2}$ as n tends to infinity. Our final result is a stability theorem for complete multipartite graphs G, describing the asymptotic structure of such G with F(G;k) = F(n;k) · 2o(n2) in terms of solutions to the optimisation problem.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 163 , Issue 2 , September 2017 , pp. 341 - 356
Copyright
Copyright © Cambridge Philosophical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Alon, N., Balogh, J., Keevash, P. and Sudakov, B. The number of edge colorings with no monochromatic cliques. J. London Math. Soc. 70 (2004), 273–288.Google Scholar
[2] Alon, N. and Yuster, R. The number of orientations having no fixed tournament. Combinatorica 26 (2006), 1–16.CrossRefGoogle Scholar
[3] Balogh, J. A remark on the number of edge colorings of graphs. Europ. J. Comb. 27 (2006), 565–573.CrossRefGoogle Scholar
[4] Benevides, F. S., Hoppen, C. and Sampaio, R. M. Edge-colorings of graphs avoiding complete graphs with a prescibed coloring, preprint (arXiv:1605.08013).Google Scholar
[5] Erdős, P. Some new applications of probability methods to combinatorial analysis and graph theory Proceedings of the Fifth Southeastern Conference on Combinatorics, Graph Theory and Computing, Congress Numerantium X (1974), 39–51.Google Scholar
[6] Erdős, P. Some of my favorite problems in various branches of combinatorics. Matematiche (Catania) 47 (1992), 231–240.Google Scholar
[7] Hoppen, C., Kohayakawa, Y. and Lefmann, H. Kneser colorings of uniform hypergraphs. Elec. Notes in Disc. Math. 34 (2009), 219–223.Google Scholar
[8] Hoppen, C., Kohayakawa, Y. and Lefmann, H. Edge colourings of graphs avoiding monochromatic matchings of a given size. Comb. Prob. Comp. 21 (2012), 203–218.CrossRefGoogle Scholar
[9] Hoppen, C., Kohayakawa, Y. and Lefmann, H. Edge-colorings of graphs avoiding fixed monochromatic subgraphs with linear Turán number. Europ. J. Comb. 35 (2014), 354–373.Google Scholar
[10] Hoppen, C. and Lefmann, H. Edge-colorings avoiding a fixed matching with a prescribed color pattern. Europ. J. Comb. 47 (2015), 75–94.Google Scholar
[11] Hoppen, C., Lefmann, H. and Odermann, K. A coloring problem for intersecting vector spaces. Disc. Math. 339 (2016), 2941–2954.Google Scholar
[12] Hoppen, C., Lefmann, H., Odermann, K. and Sanches, J. Edge-colorings avoiding fixed rainbow stars, Elec. Notes in Disc. Math. 50 (2015), 275–280.Google Scholar
[13] Komlós, J. and Simonovits, M. ‘Szemerédi's regularity lemma and its applications to graph theory’ in Combinatorics, Paul Erdős is Eighty. Miklós, D., Sós, V. T. and Szőni, T., Eds., vol. 2 (Bolyai Math. Soc., 1996), pp. 295–352.Google Scholar
[14] Lefmann, H., Person, Y., Rödl, V. and Schacht, M. On colorings of hypergraphs without monochromatic Fano planes. Comb. Prob. Comp. 18 (2009), 803–818.Google Scholar
[15] Lefmann, H., Person, Y. and Schacht, M. A structural result for hypergraphs with many restricted edge colorings. J. Comb. 1 (2010), 441-475.Google Scholar
[16] Pikhurko, O. and Yilma, Z. The maximum number of K 3-free and K 4-free edge 4-colorings. J. London Math. Soc. 85 (2012), 593–615.Google Scholar
[17] Szemerédi, E. Regular partitions of graphs Proc. Colloq. Int. CNRS (Paris, 1976), pp. 309–401.Google Scholar
[18] Turán, P. On an extremal problem in graph theory (in Hungarian). Mat. Fiz. Lapok 48 (1941), 436–452.Google Scholar
[19] Xu, X., Shao, Z., Su, W. and Li, Z. Set-coloring of edges and multigraph Ramsey numbers. Graphs. Comb. 25 (2009), 863–870.Google Scholar
[20] Yuster, R. The number of edge colorings with no monochromatic triangle. J. Graph Theory 21 (1996), 441–452.Google Scholar
[21] Zykov, A. A. On some properties of linear complexes (in Russian). Mat. Sbornik N.S. 24 (1949), 163–188.Google Scholar