Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Morozov, Oleg I.
and
Sergyeyev, Artur
2014.
The four-dimensional Martínez Alonso–Shabat equation: Reductions and nonlocal symmetries.
Journal of Geometry and Physics,
Vol. 85,
Issue. ,
p.
40.
Kryński, Wojciech
2014.
Webs and projective structures on a plane.
Differential Geometry and its Applications,
Vol. 37,
Issue. ,
p.
133.
Kryński, Wojciech
2014.
Remarks on the Jacobi endomorphisms and the Cartan invariants of ODEs.
International Journal of Geometric Methods in Modern Physics,
Vol. 11,
Issue. 10,
p.
1450080.
Dunajski, Maciej
2014.
Summary of session A4: Complex and conformal methods in classical and quantum gravity.
General Relativity and Gravitation,
Vol. 46,
Issue. 5,
Kryński, Wojciech
2016.
Paraconformal structures, ordinary differential equations and totally geodesic manifolds.
Journal of Geometry and Physics,
Vol. 103,
Issue. ,
p.
1.
KRYŃSKI, WOJCIECH
2016.
Webs and the Plebański equation.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 161,
Issue. 3,
p.
455.
Dunajski, Maciej
Gutowski, Jan
and
Sabra, Wafic
2017.
Einstein–Weyl spaces and near-horizon geometry.
Classical and Quantum Gravity,
Vol. 34,
Issue. 4,
p.
045009.
Randall, Matthew
2017.
Three dimensional near-horizon metrics that are Einstein-Weyl.
Archivum Mathematicum,
p.
335.
Prykarpatski, Anatolij
Hentosh, Oksana
and
Prykarpatsky, Yarema
2017.
Geometric Structure of the Classical Lagrange-d’Alambert Principle and Its Application to Integrable Nonlinear Dynamical Systems.
Mathematics,
Vol. 5,
Issue. 4,
p.
75.
Kruglikov, Boris
and
Panasyuk, Andriy
2017.
Veronese webs and nonlinear PDEs.
Journal of Geometry and Physics,
Vol. 115,
Issue. ,
p.
45.
Krasil’shchik, Joseph
Verbovetsky, Alexander
and
Vitolo, Raffaele
2017.
The Symbolic Computation of Integrability Structures for Partial Differential Equations.
p.
105.
Kryński, Wojciech
2018.
On deformations of the dispersionless Hirota equation.
Journal of Geometry and Physics,
Vol. 127,
Issue. ,
p.
46.
Doubrov, Boris
Ferapontov, Evgeny V.
Kruglikov, Boris
and
Novikov, Vladimir S.
2018.
On integrability in Grassmann geometries: integrable systems associated with fourfolds in Gr(3,5).
Proceedings of the London Mathematical Society,
Vol. 116,
Issue. 5,
p.
1269.
Dunajski, Maciej
Gutowski, Jan
and
Sabra, Wafic
2018.
A note on the Hyper-CR equation, and gauged N= 2 supergravity.
Physics Letters B,
Vol. 780,
Issue. ,
p.
166.
Baran, H.
Krasilshchik, I. S.
Morozov, O. I.
and
Vojčák, P.
2018.
Nonlocal Symmetries of Integrable Linearly Degenerate Equations: A Comparative Study.
Theoretical and Mathematical Physics,
Vol. 196,
Issue. 2,
p.
1089.
Krasil’shchik, I.S.
Morozov, O.I.
and
Vojčák, P.
2019.
Nonlocal symmetries, conservation laws, and recursion operators of the Veronese web equation.
Journal of Geometry and Physics,
Vol. 146,
Issue. ,
p.
103519.
Kumar, Sachin
and
Kumar, Amit
2019.
Lie symmetry reductions and group invariant solutions of (2 + 1)-dimensional modified Veronese web equation.
Nonlinear Dynamics,
Vol. 98,
Issue. 3,
p.
1891.
Klemm, Dietmar Silke
and
Ravera, Lucrezia
2019.
Supersymmetric near-horizon geometry and Einstein-Cartan-Weyl spaces.
Physics Letters B,
Vol. 793,
Issue. ,
p.
265.
Hentosh, Oksana
and
Prykarpatsky, Yarema
2020.
The Lax–Sato integrable heavenly equations on functional supermanifolds and their Lie-algebraic structure.
European Journal of Mathematics,
Vol. 6,
Issue. 1,
p.
232.
FERAPONTOV, EVGENY
and
KRUGLIKOV, BORIS
2021.
Dispersionless integrable hierarchies andGL(2, ℝ) geometry.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 170,
Issue. 1,
p.
129.
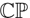 $T\mathbb{CP}^1$, and how to recover the pencil of Poisson structures in five dimensions illustrating the method by an example of the Veronese web on the Heisenberg group.
$T\mathbb{CP}^1$, and how to recover the pencil of Poisson structures in five dimensions illustrating the method by an example of the Veronese web on the Heisenberg group.

